
【题目】如图,AB是⊙O的直径,点C为AB上一点,作CD⊥AB交⊙O于D,连接AD,将△ACD沿AD翻折至△AC′D.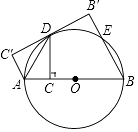
(1)请你判断C′D与⊙O的位置关系,并说明理由;
(2)过点B作BB′⊥C′D′于B′,交⊙O于E,若CD= ![]() ,AC=3,求BE的长.
,AC=3,求BE的长.
【答案】
(1)解:C′D是⊙O的切线,
理由:连接OD,
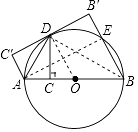
∵OD=OA,
∴∠OAD=∠ADO,
∵将△ACD沿AD翻折至△AC′D,
∴∠C′DA=∠CDA,
∵CD⊥AB,
∴∠DAC+∠ADC=90°,
∴∠ADO+∠C′DA=90°,
∴OD⊥C′D,
∴C′D是⊙O的切线
(2)解:连接AE,BD,
∵AB是⊙O的直径,
∴AE⊥BE,AD⊥BD,
∵BB′⊥C′D′,
∴∠C′=∠B′=∠AEB′=90°,
∴四边形AEB′C′是矩形,
∴AC′=B′E,AE=C′B′,
∵将△ACD沿AD翻折至△AC′D,
∵AC′=AC=3,C′D=CD= ![]() ,
,
∵AC′⊥C′B′,OD⊥C′B′,
∴AC′∥OD∥BB′,
∵AO=BO,
∴C′B′=2C′D=2 ![]() ,
,
∴AE=2 ![]() ,
,
∵DC⊥AB,
∴CD2=ACCB,
∴CB=7,
∴AB=10,
∴BE= ![]() =4.
=4.
【解析】(1)连接OD,根据等腰三角形的性质得到∠OAD=∠ADO,根据折叠的性质得到∠C′DA=∠CDA,于是得到结论;
(2)连接AE,BD,由AB是⊙O的直径,得到AE⊥BE,AD⊥BD,推出四边形AEB′C′是矩形,得到AC′=B′E,AE=C′B′,根据折叠的性质得到AC′=AC=3,C′D=CD=![]() ,根据平行线等分线段定理得到AO=BO,得到AE的值,根据射影定理得到CB=7,由勾股定理即可得到BE的长.
,根据平行线等分线段定理得到AO=BO,得到AE的值,根据射影定理得到CB=7,由勾股定理即可得到BE的长.
【考点精析】认真审题,首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2),还要掌握垂径定理(垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】如图,已知直线y=x+k和双曲线y= ![]() (k为正整数)交于A,B两点.
(k为正整数)交于A,B两点.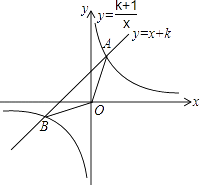
(1)当k=1时,求A、B两点的坐标;
(2)当k=2时,求△AOB的面积;
(3)当k=1时,△OAB的面积记为S1 , 当k=2时,△OAB的面积记为S2 , …,依此类推,当k=n时,△OAB的面积记为Sn , 若S1+S2+…+Sn= ![]() ,求n的值.
,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y= ![]() (x>0)的图象交于A(m,6),B(3,n)两点,与x轴交于点C,与y轴交于点D,下列结论:①一次函数解析式为y=﹣2x+8;②AD=BC;③kx+b﹣
(x>0)的图象交于A(m,6),B(3,n)两点,与x轴交于点C,与y轴交于点D,下列结论:①一次函数解析式为y=﹣2x+8;②AD=BC;③kx+b﹣ ![]() <0的解集为0<x<1或x>3;④△AOB的面积是8,其中正确结论的个数是( )
<0的解集为0<x<1或x>3;④△AOB的面积是8,其中正确结论的个数是( )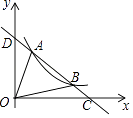
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题有( )
①直线外一点与直线上各点连接的所有线段中,垂线段最短;
②三角形的一个外角大于任何一个内角;
③如果∠1和∠2是对顶角,那么![]() ;
;
④如果一条直线和两条直线中的一条垂直,那么这条直线也和另一条垂直.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,过点A引射线AH,交边CD于点H(点H与点D不重合).通过翻折,使点B落在射线AH上的点G处,折痕AE交BC于E,延长EG交CD于F.
(感知)(1)如图①,当点H与点C重合时,猜想FG与FD的数量关系,并说明理由.
(探究)(2)如图②,当点H为边CD上任意一点时,(1)中结论是否仍然成立?请说明理由.
(应用)(3)在图②中,当DF=3,CE=5时,直接利用探究的结论,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和,如23=3+5,33=7+9+11,43=13+15+17+19,…若m3分裂后,其中有一个奇数是2015,则m的值是( )
A.43B.44C.45D.46
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2AD,点E,F分别是AB,BC边的中点,连接AF,CE交于点M,连接BM并延长交CD于点N,连接DE交AF于点P,则结论:①∠ABN=∠CBN;②DE∥BN;③△CDE是等腰三角形;④EM:BE= ![]() :3;⑤S△EPM=
:3;⑤S△EPM= ![]() S梯形ABCD , 正确的个数有( )
S梯形ABCD , 正确的个数有( )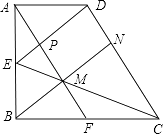
A.5个
B.4个
C.3个
D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点C(﹣3,0),点A,B分别在x轴,y轴的正半轴上,且满足 ![]() +|OA﹣1|=0
+|OA﹣1|=0
(1)求点A,点B的坐标.
(2)若点P从C点出发,以每秒1个单位的速度沿射线CB运动,连结AP.设△ABP的面积为S,点P的运动时间为t秒,求S与t的函数关系式,并写出自变量的取值范围.
(3)在(2)的条件下,是否存在点P,使以点A,B,P为顶点的三角形与△AOB相似?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如下表:
原进价 | 零售价 | |
餐桌 | a | 270 |
餐椅 | b | 70 |
若购进4张餐桌19张餐椅需要1360元;若购进6张餐桌26张餐椅需要1940元.
![]() 求表中a,b的值;
求表中a,b的值;
![]() 今年年初由于原材料价格上涨,每张餐桌的进价上涨了10元,每张餐椅的进价上涨了
今年年初由于原材料价格上涨,每张餐桌的进价上涨了10元,每张餐椅的进价上涨了![]() ,商场决定购进餐桌30张,餐椅170张进行销售,全部售出后,要求利润不低于7380元,求m的最大值.
,商场决定购进餐桌30张,餐椅170张进行销售,全部售出后,要求利润不低于7380元,求m的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com