
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬µćC£Ø©3£¬0£©£¬µćA£¬B·Ö±šŌŚxÖį£¬yÖįµÄÕż°ėÖįÉĻ£¬ĒŅĀś×ć ![]() +|OA©1|=0
+|OA©1|=0
£Ø1£©ĒóµćA£¬µćBµÄ×ų±ź£®
£Ø2£©ČōµćP“ÓCµć³ö·¢£¬ŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČŃŲÉäĻßCBŌĖ¶Æ£¬Į¬½įAP£®Éč”÷ABPµÄĆ껿ĪŖS£¬µćPµÄŌĖ¶ÆŹ±¼äĪŖtĆė£¬ĒóSÓėtµÄŗÆŹż¹ŲĻµŹ½£¬²¢Š“³ö×Ō±äĮæµÄȔֵ·¶Ī§£®
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬ŹĒ·ń“ęŌŚµćP£¬Ź¹ŅŌµćA£¬B£¬PĪŖ¶„µćµÄČż½ĒŠĪÓė”÷AOBĻąĖĘ£æČō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öµćPµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ
£Ø1£©½ā£ŗ”ß ![]() +|OA©1|=0
+|OA©1|=0
”ąOA©1=0”¢OB2©3=0£¬
”ąOA=1”¢OB= ![]() £¬
£¬
”ąµćAµÄ×ų±źĪŖ£Ø1£¬0£©”¢BµÄ×ų±ź£Ø0£¬ ![]() £©
£©

£Ø2£©½ā£ŗ”ßC£Ø©3£¬0£©£¬B£Ø0£¬ ![]() £©£»
£©£»
”ąOC=3£¬OB= ![]()
ŌŚRT”÷BOCÖŠ£¬BC= ![]() =2
=2 ![]() £¬
£¬
ÉčµćAµ½Ö±ĻßCBµÄ¾ąĄėĪŖy£¬Ōņ
![]() ”Į2
”Į2 ![]() y=
y= ![]() ”Į£Ø3+1£©”Į
”Į£Ø3+1£©”Į ![]() £¬
£¬
½āµĆy=2£®
ŌņS= ![]() ”Į|2
”Į|2 ![]() ©t|”Į2=|2
©t|”Į2=|2 ![]() ©t|£®
©t|£®
¹ŹSÓėtµÄŗÆŹż¹ŲĻµŹ½ĪŖ£ŗS=©t+2 ![]() £Ø0”Üt”Ü2
£Ø0”Üt”Ü2 ![]() £©»ņS=t©2
£©»ņS=t©2 ![]() £Øt£¾2
£Øt£¾2 ![]() £©£®
£©£®
£Ø3£©½ā£ŗ“ęŌŚ£¬
ĄķÓÉ£ŗ”ßtan”ĻOBC= ![]() =
= ![]() =
= ![]() £¬
£¬
”ą”ĻOBC=60”ć£¬
”ą”ĻBCO=30”ć£¬
”ąBC=2OB=2 ![]() £¬
£¬
”ßtan”ĻOBA= ![]() =
= ![]() =
= ![]() £¬
£¬
”ą”ĻOBA=30”ć£¬
”ą”ĻABC=90”ć£¬AB=2OA=2£¬
¢Łµ±0”Üt”Ü2 ![]() Ź±£¬Čō”÷PBA”×”÷AOBŹ±£¬Ōņ
Ź±£¬Čō”÷PBA”×”÷AOBŹ±£¬Ōņ ![]() =
= ![]() £¬
£¬
¼“ ![]() =
= ![]() £¬
£¬
”ąPB= ![]() £¬
£¬
”ąPBsin60”ć= ![]() ”Į
”Į ![]() =1£¬PBcos60”ć=
=1£¬PBcos60”ć= ![]() ”Į
”Į ![]() =
= ![]() £¬
£¬
”ąP£Ø©1£¬ ![]() £©£»
£©£»
Čō”÷ABP”×”÷AOBŹ±£¬Ōņ ![]() =
= ![]() £¬
£¬
¼“ ![]() =
= ![]() £¬
£¬
”ąPB=2 ![]() £¬
£¬
”ąPBsin60”ć=2 ![]() ”Į
”Į ![]() =3£¬PBcos60”ć=2
=3£¬PBcos60”ć=2 ![]() ”Į
”Į ![]() =
= ![]() £¬
£¬
”ąP£Ø©3£¬0£©£¬
¢Śµ±t£¾2 ![]() Ź±£¬Čō”÷PBA”×”÷AOBŹ±£¬Ōņ
Ź±£¬Čō”÷PBA”×”÷AOBŹ±£¬Ōņ ![]() =
= ![]() £¬
£¬
¼“ ![]() =
= ![]() £¬
£¬
”ąPB= ![]() £¬
£¬
”ąPBsin60”ć= ![]() ”Į
”Į ![]() =1£¬PBcos60”ć=
=1£¬PBcos60”ć= ![]() ”Į
”Į ![]() =
= ![]() £¬
£¬
”ąP£Ø1£¬ ![]() £©£»
£©£»
Čō”÷ABP”×”÷AOBŹ±£¬Ōņ ![]() =
= ![]() £¬
£¬
¼“ ![]() =
= ![]() £¬
£¬
”ąPB=2 ![]() £¬
£¬
”ąPBsin60”ć=2 ![]() ”Į
”Į ![]() =3£¬PBcos60”ć=2
=3£¬PBcos60”ć=2 ![]() ”Į
”Į ![]() =
= ![]() £¬
£¬
”ąP£Ø3£¬2 ![]() £©£¬
£©£¬
ĖłŅŌ£¬“ęŌŚµćP£¬Ź¹ŅŌµćA£¬B£¬PĪŖ¶„µćµÄČż½ĒŠĪÓė”÷AOBĻąĖĘ£¬PµćµÄ×ų±źĪŖ£Ø©1£¬ ![]() £©»ņ£Ø©3£¬0£©»ņ£Ø1£¬
£©»ņ£Ø©3£¬0£©»ņ£Ø1£¬ ![]() £©»ņ£Ø3£¬2
£©»ņ£Ø3£¬2 ![]() £©£®
£©£®
”¾½āĪö”æ£Ø1£©øł¾Ż·ĒøŗŹżµÄŗĶĪŖ0£¬ĆæøöŹż¾łĪŖ0£¬µĆµ½OA”¢OBµÄ³¤£¬¼“æÉĒó³ö“š°ø£»£Ø2£©øł¾Ż¹“¹É¶ØĄķµĆµ½CBµÄ³¤¶Č£¬ŌŁøł¾ŻČż½ĒŠĪĆ껿¹«Ź½¼“æɵƵ½µćAµ½Ö±ĻßCBµÄ¾ąĄė£»ŌŁøł¾Ż”÷ABPµÄĆ껿=![]() BP
BP![]() AB£¬ÓĆtµÄ“śŹżŹ½±ķŹ¾BP¼“|
AB£¬ÓĆtµÄ“śŹżŹ½±ķŹ¾BP¼“|![]() ©t|£¬¼“æɵƵ½SÓėtµÄŗÆŹż¹ŲĻµŹ½ÓÉÓŚŹĒÉäĻßCB£¬æÉ·ÖĪŖPŌŚĻ߶ĪCBÉĻŗĶŌŚCBŃÓ³¤ĻßÉĻĮ½ÖÖĒéæö£»£Ø3£©ĻČĒóµĆ”ĻABC=90”ć£¬Č»ŗó·ÖĮ½ÖÖĒéæöĢÖĀŪ£ŗ¢Łµ±0”Üt”Ü
©t|£¬¼“æɵƵ½SÓėtµÄŗÆŹż¹ŲĻµŹ½ÓÉÓŚŹĒÉäĻßCB£¬æÉ·ÖĪŖPŌŚĻ߶ĪCBÉĻŗĶŌŚCBŃÓ³¤ĻßÉĻĮ½ÖÖĒéæö£»£Ø3£©ĻČĒóµĆ”ĻABC=90”ć£¬Č»ŗó·ÖĮ½ÖÖĒéæöĢÖĀŪ£ŗ¢Łµ±0”Üt”Ü![]() ¢Śµ±t£¾
¢Śµ±t£¾![]() , ĄūÓƶŌÓ¦±ß³É±ČĄżĮŠ³ö·½³Ģ£¬ŌŁŌĖÓĆČż½ĒŗÆŹż£¬¼“æÉĒóµĆµćPµÄ×ų±ź£®
, ĄūÓƶŌÓ¦±ß³É±ČĄżĮŠ³ö·½³Ģ£¬ŌŁŌĖÓĆČż½ĒŗÆŹż£¬¼“æÉĒóµĆµćPµÄ×ų±ź£®
”¾æ¼µć¾«Īö”æ¹ŲÓŚ±¾Ģāæ¼²éµÄČż½ĒŠĪµÄĆ껿ŗĶ¹“¹É¶ØĄķµÄøÅÄī£¬ŠčŅŖĮĖ½āČż½ĒŠĪµÄĆ껿=1/2”Įµ×”Įøߣ»Ö±½ĒČż½ĒŠĪĮ½Ö±½Ē±ßa”¢bµÄĘ½·½ŗĶµČÓŚŠ±±ßcµÄĘ½·½,¼“;a2+b2=c2²ÅÄÜµĆ³öÕżČ·“š°ø£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
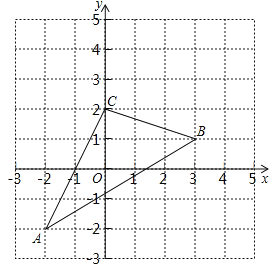
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCŌŚÖ±½Ē×ų±źĻµÖŠ£®
£Ø1£©Čō°Ń”÷ABCĻņÉĻĘ½ŅĘ2øöµ„Ī»£¬ŌŁĻņ×óĘ½ŅĘ1øöµ„Ī»µĆµ½”÷A1B1C1£¬»³ö”÷A1B1C1£¬²¢Š“³öµćA1£¬B1£¬C1µÄ×ų±ź£»
£Ø2£©Ēó”÷ABCµÄĆ껿£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ABŹĒ”ŃOµÄÖ±¾¶£¬µćCĪŖABÉĻŅ»µć£¬×÷CD”ĶAB½»”ŃOÓŚD£¬Į¬½ÓAD£¬½«”÷ACDŃŲAD·ÕŪÖĮ”÷AC”äD£®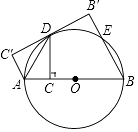
£Ø1£©ĒėÄćÅŠ¶ĻC”äDÓė”ŃOµÄĪ»ÖĆ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£»
£Ø2£©¹żµćB×÷BB”ä”ĶC”äD”äÓŚB”䣬½»”ŃOÓŚE£¬ČōCD= ![]() £¬AC=3£¬ĒóBEµÄ³¤£®
£¬AC=3£¬ĒóBEµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æA£¬B£¬CČżĆū“óѧɜ¾ŗŃ”ĻµŃ§Éś»įÖ÷ĻÆ£¬ĖūĆĒµÄ±ŹŹŌ³É¼ØŗĶæŚŹŌ³É¼Ø£Øµ„Ī»£ŗ·Ö£©·Ö±šÓĆĮĖĮ½ÖÖ·½Ź½½ųŠŠĮĖĶ³¼Ę£¬Čē±ķŗĶĶ¼Ņ»£ŗ
A | B | C | |
±ŹŹŌ | 85 | 95 | 90 |
æŚŹŌ | 80 | 85 |
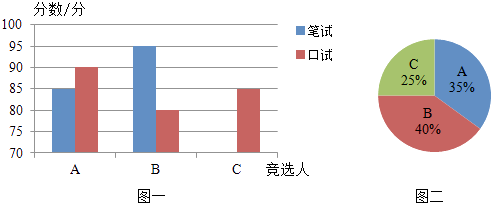
£Ø1£©Ēė½«±ķŅ»ŗĶĶ¼Ņ»ÖŠµÄæÕȱ²æ·Ö²¹³äĶźÕū£®
£Ø2£©¾ŗŃ”µÄ×īŗóŅ»øö³ĢŠņŹĒÓɱ¾ĻµµÄ300Ćūѧɜ½ųŠŠĶ¶Ę±£¬ČżĪ»ŗņŃ”ČĖµÄµĆʱĒéæöČēĶ¼¶ž£ØƻӊʜČØʱ£¬ĆæĆūѧɜֻÄÜĶĘ¼öŅ»øö£©£¬Ēė¼ĘĖćĆæČĖµÄµĆʱŹż£®
£Ø3£©ČōĆæʱ¼Ę1·Ö£¬ĻµĄļ½«±ŹŹŌ”¢æŚŹŌ”¢µĆʱȿĻī²āŹŌµĆ·Ö°“4£ŗ3£ŗ3µÄ±ČĄżČ·¶ØøöČĖ³É¼Ø£¬Ēė¼ĘĖćČżĪ»ŗņŃ”ČĖµÄ×īŗó³É¼Ø£¬²¢øł¾Ż³É¼ØÅŠ¶ĻĖÄܵ±Ń”£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĮāŠĪABCDÖŠ£¬”ĻABC=60”ć£¬EŹĒ¶Ō½ĒĻßACÉĻŅ»µć£¬FŹĒĻ߶ĪBCŃÓ³¤ĻßÉĻŅ»µć£¬ĒŅCF=AE£¬Į¬½ÓBE”¢EF£®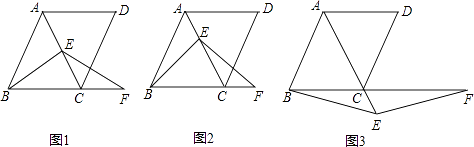
£Ø1£©ČōEŹĒĻ߶ĪACµÄÖŠµć£¬ČēĶ¼1£¬Ņ×Ö¤£ŗBE=EF£Ø²»ŠčÖ¤Ć÷£©£»
£Ø2£©ČōEŹĒĻ߶ĪAC»ņACŃÓ³¤ĻßÉĻµÄČĪŅāŅ»µć£¬ĘäĖüĢõ¼ž²»±ä£¬ČēĶ¼2”¢Ķ¼3£¬Ļ߶ĪBE”¢EFÓŠŌõŃłµÄŹżĮæ¹ŲĻµ£¬Ö±½ÓŠ“³öÄćµÄ²ĀĻė£»²¢Ń”ŌńŅ»ÖÖĒéæöøųÓčÖ¤Ć÷£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾µÄ¶ž“ĪŗÆŹż ![]() µÄĶ¼ĻóÖŠ£¬¹Ū²ģµĆ³öĮĖĻĀĆęĪåĢõŠÅĻ¢£ŗ
µÄĶ¼ĻóÖŠ£¬¹Ū²ģµĆ³öĮĖĻĀĆęĪåĢõŠÅĻ¢£ŗ
¢Ł ![]() £»¢Ś
£»¢Ś ![]() £»¢Ū
£»¢Ū ![]() £»¢Ü
£»¢Ü ![]() £»¢Ż
£»¢Ż ![]() £¬
£¬
ÄćČĻĪŖĘäÖŠÕżČ·ŠÅĻ¢µÄøöŹżÓŠøö. 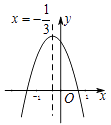
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻß ![]() Óė
Óė ![]() Öį½»ÓŚ
Öį½»ÓŚ ![]() ”¢
”¢ ![]() Į½µć£Øµć
Į½µć£Øµć ![]() ŌŚµć
ŌŚµć ![]() µÄ×ó²ą£©£¬µć
µÄ×ó²ą£©£¬µć ![]() µÄ×ų±źĪŖ
µÄ×ų±źĪŖ ![]() £¬Óė
£¬Óė ![]() Öį½»ÓŚµć
Öį½»ÓŚµć ![]() £¬×÷Ö±Ļß
£¬×÷Ö±Ļß ![]() £®¶Æµć
£®¶Æµć ![]() ŌŚ
ŌŚ ![]() ÖįÉĻŌĖ¶Æ£¬¹żµć
ÖįÉĻŌĖ¶Æ£¬¹żµć ![]() ×÷
×÷ ![]() Öį£¬½»Å×ĪļĻßÓŚµć
Öį£¬½»Å×ĪļĻßÓŚµć ![]() £¬½»Ö±Ļß
£¬½»Ö±Ļß ![]() ÓŚµć
ÓŚµć ![]() £¬Éčµć
£¬Éčµć ![]() µÄŗį×ų±źĪŖ
µÄŗį×ų±źĪŖ ![]() £®
£®
£Ø¢ń£©ĒóÅ×ĪļĻߵĽāĪöŹ½ŗĶÖ±Ļß ![]() µÄ½āĪöŹ½£»
µÄ½āĪöŹ½£»
£Ø¢ņ£©µ±µć ![]() ŌŚĻ߶Ī
ŌŚĻ߶Ī ![]() ÉĻŌĖ¶ÆŹ±£¬ĒóĻ߶Ī
ÉĻŌĖ¶ÆŹ±£¬ĒóĻ߶Ī ![]() µÄ×ī“óÖµ£»
µÄ×ī“óÖµ£»
£Ø¢ó£©µ±ŅŌ ![]() ”¢
Ӣ ![]() Ӣ
Ӣ ![]() Ӣ
”¢ ![]() ĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪŹ±£¬Ö±½ÓŠ“³ö
ĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪŹ±£¬Ö±½ÓŠ“³ö ![]() µÄÖµ£®
µÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»øö²»ĶøĆ÷µÄæŚ“ü֊װӊ4øöĶźČ«ĻąĶ¬µÄŠ”Ēņ£¬·Ö±š±źÓŠŹż×Ö1£¬2£¬3£¬4£¬ĮķĶāÓŠŅ»øöæÉŅŌ×ŌÓÉŠż×ŖµÄŌ²ÅĢ£¬±»·Ö³ÉĆ껿ĻąµČµÄ3øöÉČŠĪĒųÓņ£¬·Ö±š±źÓŠŹż×Ö1£¬2£¬3£ØČēĶ¼ĖłŹ¾£©£®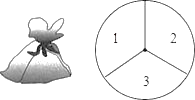
£Ø1£©“ÓæŚ“üÖŠĆž³öŅ»øöŠ”Ēņ£¬ĖłĆžĒņÉĻµÄŹż×Ö“óÓŚ2µÄøÅĀŹĪŖ£»
£Ø2£©Š”ĮśŗĶŠ”¶«ĻėĶعżÓĪĻ·Ą“¾ö¶ØĖ“ś±ķѧŠ£²Ī¼ÓøčÓ½±ČČü£¬ÓĪĻ·¹ęŌņĪŖ£ŗŅ»ČĖ“ÓæŚ“üÖŠĆž³öŅ»øöŠ”Ēņ£¬ĮķŅ»ČĖ×Ŗ¶ÆŌ²ÅĢ£¬Čē¹ūĖłĆžĒņÉĻµÄŹż×ÖÓėŌ²ÅĢÉĻ×Ŗ³öŹż×ÖÖ®ŗĶŠ”ÓŚ5£¬ÄĒĆ“Š”ĮśČ„£»·ńŌņŠ”¶«Č„£®ÄćČĻĪŖÓĪĻ·¹«Ę½Āš£æĒėÓĆŹ÷דĶ¼»ņĮŠ±ķ·ØĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬CD”ĶABÓŚD£¬µćFŹĒBCÉĻČĪŅāŅ»µć£¬FE”ĶABÓŚE£¬ĒŅ”Ļ1£½”Ļ2£®ĒóÖ¤£ŗ”Ļ3=”ĻACB£®
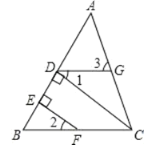
ĻĀĆęøų³öĮĖ²æ·ÖÖ¤Ć÷¹ż³ĢŗĶĄķÓÉ£¬Ēė²¹Č«ĖłÓŠÄŚČŻ£®
Ö¤Ć÷£ŗ”ßCD”ĶAB£¬FE”ĶAB
”ą”ĻBDC=”ĻBEF=90”ć£Ø £©
”ąEF”ĪDC£Ø £©
”ą”Ļ2= £Ø £©
Ó֔ߔĻ2=”Ļ1£ØŅŃÖŖ£©
”ą”Ļ1= £ØµČĮæ“ś»»£©
”ąDG”ĪBC£Ø £©
”ą”Ļ3=”ĻACB£ØĮ½Ö±ĻßĘ½ŠŠ£¬Ķ¬Ī»½ĒĻąµČ£©
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com