
【题目】在菱形ABCD中,∠ABC=60°,E是对角线AC上一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.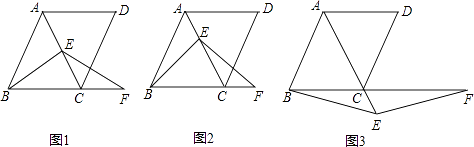
(1)若E是线段AC的中点,如图1,易证:BE=EF(不需证明);
(2)若E是线段AC或AC延长线上的任意一点,其它条件不变,如图2、图3,线段BE、EF有怎样的数量关系,直接写出你的猜想;并选择一种情况给予证明.
【答案】
(1)证明:∵四边形ABCD为菱形,
∴AB=BC,
又∵∠ABC=60°,
∴△ABC是等边三角形,
∵E是线段AC的中点,
∴∠CBE= ![]() ∠ABC=30°,AE=CE,
∠ABC=30°,AE=CE,
∵AE=CF,
∴CE=CF,
∴∠F=∠CEF,
∵∠F+∠CEF=∠ACB=60°,
∴∠F=30°,
∴∠CBE=∠F,
∴BE=EF;
(2)证明:图2:BE=EF.
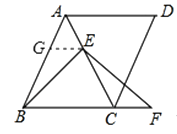
图3:BE=EF.

图2证明如下:过点E作EG∥BC,交AB于点G,
∵四边形ABCD为菱形,
∴AB=BC,
又∵∠ABC=60°,
∴△ABC是等边三角形,
∴AB=AC,∠ACB=60°,
又∵EG∥BC,
∴∠AGE=∠ABC=60°,
又∵∠BAC=60°,
∴△AGE是等边三角形
∴AG=AE,
∴BG=CE,
又∵CF=AE,
∴GE=CF,
又∵∠BGE=∠ECF=120°,
∴△BGE≌△ECF(SAS),
∴BE=EF;
图3证明如下:过点E作EG∥BC交AB延长线于点G,
∵四边形ABCD为菱形,
∴AB=BC,
又∵∠ABC=60°,
∴△ABC是等边三角形,
∴AB=AC,∠ACB=60°,
又∵EG∥BC,
∴∠AGE=∠ABC=60°,
又∵∠BAC=60°,
∴△AGE是等边三角形,
∴AG=AE,
∴BG=CE,
又∵CF=AE,
∴GE=CF,
又∵∠BGE=∠ECF=60°,
∴△BGE≌△ECF(SAS),
∴BE=EF.
【解析】(1)根据菱形的性质结合∠ABC=60°可得△ABC是等边三角形,再根据等腰三角形三线合一的性质可得∠CBE=![]() ∠ABC=30°,AE=CE,所以CE=CF,然后由等边对等角的性质可得∠F=∠CEF,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠F=30°,从而得到∠CBE=∠F,根据等角对等边的性质即可证明;(2)图2,过点E作EG∥BC,构造全等三角形△BGE≌△ECF,由已知可得BG=CE,GE=CF,∠BGE=∠ECF=120°,可证明△BGE和△ECF 全等,根据全等三角形对应边相等即可得证;图3,证明思路与方法与图2完全相同.
∠ABC=30°,AE=CE,所以CE=CF,然后由等边对等角的性质可得∠F=∠CEF,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠F=30°,从而得到∠CBE=∠F,根据等角对等边的性质即可证明;(2)图2,过点E作EG∥BC,构造全等三角形△BGE≌△ECF,由已知可得BG=CE,GE=CF,∠BGE=∠ECF=120°,可证明△BGE和△ECF 全等,根据全等三角形对应边相等即可得证;图3,证明思路与方法与图2完全相同.
【考点精析】通过灵活运用菱形的性质,掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,ABCD中,BD⊥AD,∠A=45°,E、F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.

(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,过点A引射线AH,交边CD于点H(点H与点D不重合).通过翻折,使点B落在射线AH上的点G处,折痕AE交BC于E,延长EG交CD于F.
(感知)(1)如图①,当点H与点C重合时,猜想FG与FD的数量关系,并说明理由.
(探究)(2)如图②,当点H为边CD上任意一点时,(1)中结论是否仍然成立?请说明理由.
(应用)(3)在图②中,当DF=3,CE=5时,直接利用探究的结论,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2AD,点E,F分别是AB,BC边的中点,连接AF,CE交于点M,连接BM并延长交CD于点N,连接DE交AF于点P,则结论:①∠ABN=∠CBN;②DE∥BN;③△CDE是等腰三角形;④EM:BE= ![]() :3;⑤S△EPM=
:3;⑤S△EPM= ![]() S梯形ABCD , 正确的个数有( )
S梯形ABCD , 正确的个数有( )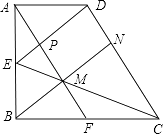
A.5个
B.4个
C.3个
D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=120°,S△ABC=8![]() ,点M,P,N分别是边AB,BC,AC上任意一点,则:
,点M,P,N分别是边AB,BC,AC上任意一点,则:
(1)AB的长为____________.
(2)PM+PN的最小值为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点C(﹣3,0),点A,B分别在x轴,y轴的正半轴上,且满足 ![]() +|OA﹣1|=0
+|OA﹣1|=0
(1)求点A,点B的坐标.
(2)若点P从C点出发,以每秒1个单位的速度沿射线CB运动,连结AP.设△ABP的面积为S,点P的运动时间为t秒,求S与t的函数关系式,并写出自变量的取值范围.
(3)在(2)的条件下,是否存在点P,使以点A,B,P为顶点的三角形与△AOB相似?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线 ![]() 的对称轴为直线
的对称轴为直线 ![]() ,与
,与 ![]() 轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论: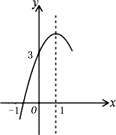
① ![]() ;② 方程
;② 方程 ![]() 的两个根是
的两个根是 ![]() ;③
;③ ![]() ;④当
;④当 ![]() 时,
时, ![]() 的取值范围是
的取值范围是 ![]() ;⑤ 当
;⑤ 当 ![]() 时,
时, ![]() 随
随 ![]() 增大而增大;其中结论正确有.
增大而增大;其中结论正确有.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=﹣![]() x+m交折线OAB于点E.
x+m交折线OAB于点E.
(1)请写出m的取值范围 ;
(2)记△ODE的面积为S,求S与m的函数关系式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com