
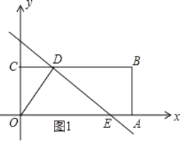
【题目】如图所示,四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=﹣![]() x+m交折线OAB于点E.
x+m交折线OAB于点E.
(1)请写出m的取值范围 ;
(2)记△ODE的面积为S,求S与m的函数关系式.

【答案】(1)1<m<2.5;(2)S=![]()
【解析】
(1)利用一次函数图象上点的坐标特征可求出点D的坐标,根据点D横坐标的范围即可得出m的取值范围;
(2)分点E在线段OA上及点E在线段AB上时(与端点A、B不重合)两种情况考虑:①当点E在线段OA上时,利用一次函数图象上点的坐标特征可求出点E的坐标,由点E的横坐标≤3可得出此时m的取值范围,再利用三角形的面积公式可找出S关于m的函数关系式;②当点E在线段AB上时(与端点A、B不重合),此时1.5<m<2.5,利用一次函数图象上点的坐标特征可求出点E的坐标,结合点D、B的坐标即可得出CD、AE、BD、BE的长度,再根据S=S矩形OABC-S△OAE-S△OCD-S△BDE即可找出S关于m的函数关系式.综上即可得出结论.
解:(1)当y=1时,有﹣![]() x+m=1,
x+m=1,
∴x=2m﹣2,
∴点D的坐标为(2m﹣2,1).
∵点D是线段BC上的动点(与端点B、C不重合),
∴0<2m﹣2<3,
∴1<m<2.5.
故答案为:1<m<2.5.
(2)①当点E在线段OA上时,如图1所示.
当y=0时,有﹣![]() x+m=0,
x+m=0,
∴x=2m,
∴点E的坐标为(2m,0),
∴2m≤3,
∴此时1<m≤1.5,S=![]() OE OC=m;
OE OC=m;
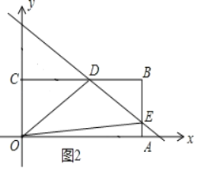
②当点E在线段AB上时(与端点A、B不重合),此时1.5<m<2.5,如图2所示.
当x=3时,y=﹣![]() x+m=m﹣1.5,
x+m=m﹣1.5,
∴点E的坐标为(3,m﹣1.5).
∵点D的坐标为(2m﹣2,1),点B的坐标为(3,1),
∴CD=2m﹣2,BD=5﹣2m,AE=m﹣1.5,BE=2.5﹣m,
S=S矩形OABC﹣S△OAE﹣S△OCD﹣S△BDE,
=OAOC﹣![]() OAAE﹣
OAAE﹣![]() OCCD﹣
OCCD﹣![]() BDBE,
BDBE,
=3×1﹣![]() ×3(m﹣1.5
×3(m﹣1.5![]() (2m﹣2)﹣
(2m﹣2)﹣![]() (5﹣2m)(2.5﹣m),
(5﹣2m)(2.5﹣m),
=﹣m2+2.5m.
综上所述:S与m的函数关系式为S=![]() .
.


科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠ABC=60°,E是对角线AC上一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.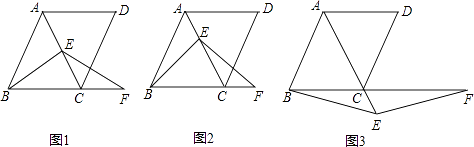
(1)若E是线段AC的中点,如图1,易证:BE=EF(不需证明);
(2)若E是线段AC或AC延长线上的任意一点,其它条件不变,如图2、图3,线段BE、EF有怎样的数量关系,直接写出你的猜想;并选择一种情况给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数 ![]() 的图象经过坐标原点,与x轴的另一个交点为A(-2,0).
的图象经过坐标原点,与x轴的另一个交点为A(-2,0).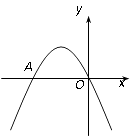
(1)求二次函数的解析式
(2)在抛物线上是否存在一点P,使△AOP的面积为3,若存在请求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=1,点D、E在直线BC上运动,设BD=x,CE=y.如果∠BAC=30°,∠DAE=105°,则y与x之间的函数关系式为.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高 ![]() m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,篮圈距地面3m.
m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,篮圈距地面3m.
(1)建立如图所示的平面直角坐标系,求抛物线的解析式并判断此球能否准确投中?
(2)此时,若对方队员乙在甲前面1m处跳起盖帽拦截,已知乙的最大摸高为3.1m,那么他能否获得成功?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD⊥AB于D,点F是BC上任意一点,FE⊥AB于E,且∠1=∠2.求证:∠3=∠ACB.
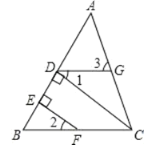
下面给出了部分证明过程和理由,请补全所有内容.
证明:∵CD⊥AB,FE⊥AB
∴∠BDC=∠BEF=90°( )
∴EF∥DC( )
∴∠2= ( )
又∵∠2=∠1(已知)
∴∠1= (等量代换)
∴DG∥BC( )
∴∠3=∠ACB(两直线平行,同位角相等)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的函数图象与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作Rt△ABC,且使∠ABC=30°.
的函数图象与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作Rt△ABC,且使∠ABC=30°.
(1)求△ABC的面积;
(2)如果在第二象限内有一点P(m,![]() ),试用含m的代数式表示△APB的面积,并求当△APB与△ABC面积相等时m的值;
),试用含m的代数式表示△APB的面积,并求当△APB与△ABC面积相等时m的值;
(3)是否存在使△QAB是等腰三角形并且在坐标轴上的点Q?若存在,请写出点Q所有可能的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副三角板直角顶点重合于点![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)如图(1),若![]() ,求证:
,求证:![]() ;
;
(2)如图(2),若![]() ,
,![]() ,则
,则![]() 度;
度;
(3)如图(3),在(1)的条件下,![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,
,![]() ,若
,若![]() ,
,![]() ,
,![]() ,求
,求![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践操作:在矩形ABCD中,AB=4,AD=3,现将纸片折叠,点D的对应点记为点P,折痕为EF(点E、F是折痕与矩形的边的交点),再将纸片还原.
初步思考:
(1)若点P落在矩形ABCD的边AB上(如图①)
①当点P与点A重合时,∠DEF= °;当点E与点A重合时,∠DEF= °;
②当点E在AB上,点F在DC上时(如图②),
求证:四边形DEPF为菱形,并直接写出当AP=3.5时的菱形EPFD的边长.

深入探究
(2)若点P落在矩形ABCD的内部(如图③),且点E、F分别在AD、DC边上,请直接写出AP的最小值 .
拓展延伸
(3)若点F与点C重合,点E在AD上,线段BA与线段FP交于点M(如图④).在各种不同的折叠位置中,是否存在某一情况,使得线段AM与线段DE的长度相等?若存在,请直接写出线段AE的长度;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com