Question

【题目】 如图，正方形ABCD中，E是AD的中点，F是AB边上的一点，连接FE并延长与CD的延长线相交于点G，作EH⊥FG交BC的延长线于点H．
（1）若BC=8，BF=5，求线段FG的长；
（2）求证：EH=2EG．

Answer 1

【答案】（1）10；（2）证明见解析.

【解析】试题分析：

试题解析：（1）∵BC=8，BF=5

∴AF=3

∵E是AD的中点，

∴AE=4

在△AFE中，EF＝＝5，

∵四边形ABCD是正方形，

∴∠A=∠EDG=90°，

∵E为AD中点，

∴AE=ED，

在△AFE和△DGE中

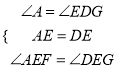
∴△AFE≌△DGE（ASA），

∴EF=EG，

∴FG=2EF=10；

（2）证明：过E作EM⊥BH于M，过G作GN⊥BA交BA的延长线于点N，

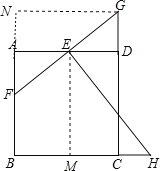
∵EH⊥FG，

∴∠HEG=90°，

∴∠H=∠FEM，

∵四边形ABCD是正方形，

∴∠DCB=90°，

∵EM⊥BC，

∴EM∥CD，

∴∠EGC=∠FEM，

∴∠H=∠EGC，

∵AB∥CD，

∴∠EGC=∠NFG

∴∠H=∠NFG，

在△NFG与△MHE中，

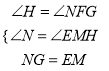
∴△NFG≌△MHE（AAS）

∴EH=FG=2EG．