
【题目】如图,在△ABC中,AB=AC,∠BAC=30°,以AC为腰在其右侧作△ACD,使AD=AC,连接BD,设∠CAD=.若=60°,CD=2,

(1)求BD的长.
(2)设∠DBC=,请你猜想与的数量关系,并说明理由.
 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】如图,甲和乙同时从学校放学,两人以各自送度匀速步行回家,甲的家在学校的正西方向,乙的家在学校的正东方向,乙家离学校的距离比甲家离学校的距离远3900米,甲准备一回家就开始做什业,打开书包时发现错拿了乙的练习册.于是立即步去追乙,终于在途中追上了乙并交还了练习册,然后再以先前的速度步行回家,(甲在家中耽搁和交还作业的时间忽略不计)结果甲比乙晚回到家中,如图是两人之间的距离y米与他们从学校出发的时间x分钟的函数关系图,则甲的家和乙的家相距_____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙3名学生各自随机选择到A、B 2个书店购书.
(1)求甲、乙2名学生在不同书店购书的概率;
(2)求甲、乙、丙3名学生在同一书店购书的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一个直径为10cm的玻璃球和一个圆锥形的牛皮纸纸帽制作一个不倒翁玩具,不倒翁的轴截面如图所示,圆锥的母线AB与⊙O相切于点B,不倒翁的顶点A到桌面L的最大距离是18cm.若将圆锥形纸帽表面全涂上颜色,则涂色部分的面积为_____cm2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,A、B为x轴上两点,C、D为y轴上的两点,经
中,A、B为x轴上两点,C、D为y轴上的两点,经
过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封
闭曲线称为“蛋线”.已知点C的坐标为(0,![]() ),点M是抛物线C2:
),点M是抛物线C2:![]() (
(![]() <0)的顶点.
<0)的顶点.

(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,![]() ,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
(1)求∠BAC的度数;
(2)当点D在AB上方,且CD⊥BP时,求证:PC=AC;
(3)在点P的运动过程中
①当点A在线段PB的中垂线上或点B在线段PA的中垂线上时,求出所有满足条件的∠ACD的度数;
②设⊙O的半径为6,点E到直线l的距离为3,连结BD,DE,直接写出△BDE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
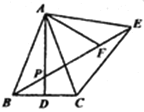
【题目】如图,在![]() 中,AB=AC,AD是BC边的中线,以AC为边作等边△ACE,BE与AD相交于点P,点F在BE上,且PF=PA,连接AF下列四个结论:①AD⊥BC;②∠ABE=∠AEB;③∠APE=60°;④△AEF≌△ABP,其中正确结论的个数是( )
中,AB=AC,AD是BC边的中线,以AC为边作等边△ACE,BE与AD相交于点P,点F在BE上,且PF=PA,连接AF下列四个结论:①AD⊥BC;②∠ABE=∠AEB;③∠APE=60°;④△AEF≌△ABP,其中正确结论的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com