
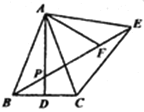
【题目】如图,在![]() 中,AB=AC,AD是BC边的中线,以AC为边作等边△ACE,BE与AD相交于点P,点F在BE上,且PF=PA,连接AF下列四个结论:①AD⊥BC;②∠ABE=∠AEB;③∠APE=60°;④△AEF≌△ABP,其中正确结论的个数是( )
中,AB=AC,AD是BC边的中线,以AC为边作等边△ACE,BE与AD相交于点P,点F在BE上,且PF=PA,连接AF下列四个结论:①AD⊥BC;②∠ABE=∠AEB;③∠APE=60°;④△AEF≌△ABP,其中正确结论的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
由等腰三角形“三线合一”的性质可得AD⊥BC,∠BAD=∠CAD,可对①进行判断;由AB=AC,△ACE是等边三角形可得AB=AE,根据等腰三角形的性质可得∠ABE=∠AEB,可对②进行判断;由三角形内角和定理可得∠ABE+∠AEB+∠BAD+∠CAD+∠CAE=180°,即可求出∠BAD+∠ABE=60°,根据外角性质可得∠APE=∠BAD+∠ABE=60°,可对③进行判断;由AP=PF,∠APE=60°可得△APF是等边三角形,可得∠APB=∠AFE=120°,利用AAS即可证明△AEF≌△ABP,可对④进行判断;综上即可得答案.
∵AB=AC,AD是BC边中线,
∴∠BAD=∠CAD,AD⊥BC,故①正确,
∵△ACE是等边三角形,
∴AC=AE,∠CAE=60°,
∴AB=AE,
∴∠ABE=∠AEB,故②正确,
∵∠ABE+∠AEB+∠BAE=180°,
∴∠ABE+∠AEB+∠BAD+∠CAD+∠CAE=180°,即2(∠BAD+∠ABE)+60°=180°,
∴∠ABE+∠BAD=60°,
∴∠APE=∠ABE+∠BAD=60°,故③正确,
∵AP=PF,∠APE=60°,
∴△APF是等边三角形,
∴∠APF=∠AFP=60°,
∴∠APB=∠AFE=120°,
在△AEF和△ABP中,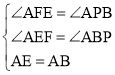 ,
,
∴△AEF≌△ABP,故④正确,
综上所述:正确的结论有①②③④,共4个,
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=30°,以AC为腰在其右侧作△ACD,使AD=AC,连接BD,设∠CAD=.若=60°,CD=2,

(1)求BD的长.
(2)设∠DBC=,请你猜想与的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,点A的坐标为![]() ,点B坐标为
,点B坐标为![]() 满足
满足![]() .
.
(1)若![]() 没有平方根,判断点A在第几象限并说明理由;
没有平方根,判断点A在第几象限并说明理由;
(2)若点A到![]() 轴的距离是点B到
轴的距离是点B到![]() 轴距离的3倍,求点B的坐标;
轴距离的3倍,求点B的坐标;
(3)点D的坐标为(4,-2),△OAB的面积是△DAB面积的2倍,求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=![]() BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=![]() BC,成立的个数有( )
BC,成立的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文化用品商店用2400元购进一批学生书包,面市后发现供不应求,商店又购进第二批同样的书包,所购数见是第一批购进数量的3倍,但单价贵了5元,结果购进第二批书包用了7800元.
(1)求第一批购进书包的单价是多少元?
(2)若商店销售这两批书包时,每个售价都是100元,全部售出后,商店共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两块等腰直角三角板△ABC和△DEC如图摆放,其中∠ACB=∠DCE=90°,F是DE的中点,H是AE的中点,G是BD的中点.
(1)如图1,若点D、E分别在AC、BC的延长线上,通过观察和测量,猜想FH和FG的数量关系为______和位置关系为______;
(2)如图2,若将三角板△DEC绕着点C顺时针旋转至ACE在一条直线上时,其余条件均不变,则(1)中的猜想是否还成立,若成立,请证明,不成立请说明理由;
(3)如图3,将图1中的△DEC绕点C顺时针旋转一个锐角,得到图3,(1)中的猜想还成立吗?直接写出结论,不用证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点坐标为A(1,2),B(2,3),C(4,1).

(1)在图中作出△ABC关于y轴对称的△A1B1C1,其中点A1的坐标为 ;
(2)将△A1B1C1向下平移4个单位得到△A2B2C2,请画出△A2B2C2,其中点B2的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将每件进价为80元的某种商品原来按每件100元出售,一天可售出100件.后来经过市场调查,发现这种商品单价每降低1元,其销量可增加10件.
(1)求商场经营该商品原来一天可获利润多少元?
(2)设后来该商品每件降价x元,,商场一天可获利润y元.
①若商场经营该商品一天要获利润2160元,则每件商品应降价多少元?
②求出y与x之间的函数关系式,结合题意写出当x取何值时,商场获利润不少于2160元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在上学的路上要经过多个路口,每个路口都设有红、黄、绿三种信号灯,假设在各路口遇到信号灯是相互独立的.
(1).如果有2个路口,求小明在上学路上到第二个路口时第一次遇到红灯的概率.(请用“画树状图”或“列表”等方法写出分析过程)
(2).如果有n个路口,则小明在每个路口都没有遇到红灯的概率是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com