
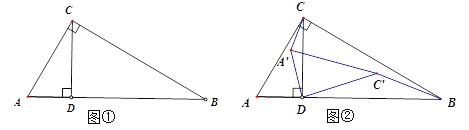
°ĺŐ‚ńŅ°Ņ»ÁÕľĘŔ£¨‘ŕRt°ųABC÷–£¨°ŌC=90°„, °ŌB=30°„,AC=1,CD°ÕAB£¨īĻ◊„ő™D£¨Ō÷Ĺę°ųACD»∆DĶ„ň≥ Ī’Ž–ż◊™![]() Ķ√ĶĹ°ųA°ģC°ĮD, –ż◊™ Īľšő™t√Ž£¨°ųACD»∆DĶ„–ż◊™ĶńĹ«ňŔ∂»
Ķ√ĶĹ°ųA°ģC°ĮD, –ż◊™ Īľšő™t√Ž£¨°ųACD»∆DĶ„–ż◊™ĶńĹ«ňŔ∂»![]() /√Ž(√Ņ√Ž◊™10∂») £ģ
/√Ž(√Ņ√Ž◊™10∂») £ģ
£®1£©–ż◊™ Īľšt= √Ž Ī£¨A°ģC°Į°őAB;
£®2£©°ųACD»∆DĶ„ň≥ Ī’Ž–ż◊™“Ľ÷‹£®3600£©£¨–ĪĪŖAC…®ĻżĶń√śĽżő™ £Ľ
£®3£©»ÁÕľĘŕ£¨Ń¨Ĺ”A°ĮC°Ę C°ĮB£ģ
ĘŔ»Ű6£ľt£ľ9£¨«ů÷§£ļ ![]() ő™∂®÷Ķ£Ľ
ő™∂®÷Ķ£Ľ
ĘŕĶĪt£ĺ9 Ī£¨…Ō ŲĹŠ¬ŘĽĻ≥…Ńʬū£Ņ»Á≥…ŃĘ÷ĪĹ”–ī≥ŲĪ»÷Ķ£¨≤Ľ≥…ŃĘ«ŽňĶ√ųņŪ”…£ģ
°ĺīūįł°Ņ£®1£©6£®2£©![]() £®3£©ĘŔ÷§√ųľŻĹ‚őŲ£ĽĘŕĹŠ¬Ř≥…ŃĘ£¨Ī»÷Ķ»‘ő™
£®3£©ĘŔ÷§√ųľŻĹ‚őŲ£ĽĘŕĹŠ¬Ř≥…ŃĘ£¨Ī»÷Ķ»‘ő™![]() .
.
°ĺĹ‚őŲ°Ņ∑÷őŲ£ļ£®1£©”…–ż◊™Ķń–ż◊™Ņ…Ķ√»Ű“™![]() °őAB,Ņ…
°őAB,Ņ…![]() ,ľīŅ…«ůĹ‚£Ľ£®2£©”…Ő‚“‚Ņ…÷™–ĪĪŖAC…®ĻżĶń√śĽżő™“‘Ķ„Dő™‘≤–ńCD£¨ACĪŖ…ŌĶńłŖő™įŽĺ∂ĶńĽ∑–ő£¨ņŻ”√īů‘≤√śĽżľű»•–°‘≤√śĽżľīŅ…«ůĹ‚£Ľ£®3£©ĘŔĶĪ6£ľt£ľ9 Ī£¨÷™60°„£ľ¶Ń£ľ90°„£¨”…°ų
,ľīŅ…«ůĹ‚£Ľ£®2£©”…Ő‚“‚Ņ…÷™–ĪĪŖAC…®ĻżĶń√śĽżő™“‘Ķ„Dő™‘≤–ńCD£¨ACĪŖ…ŌĶńłŖő™įŽĺ∂ĶńĽ∑–ő£¨ņŻ”√īů‘≤√śĽżľű»•–°‘≤√śĽżľīŅ…«ůĹ‚£Ľ£®3£©ĘŔĶĪ6£ľt£ľ9 Ī£¨÷™60°„£ľ¶Ń£ľ90°„£¨”…°ų![]() °◊°ų
°◊°ų![]() ļÕ°ų
ļÕ°ų![]() °◊°ų
°◊°ų![]() Ķ√ĶĹ
Ķ√ĶĹ![]() ő™∂®÷Ķ
ő™∂®÷Ķ![]() £ĽĘŕ”√”ŽĘŔŌŗÕ¨Ķń∑Ĺ∑®ľīŅ…Ķ√≥ŲĹŠĻŻ.
£ĽĘŕ”√”ŽĘŔŌŗÕ¨Ķń∑Ĺ∑®ľīŅ…Ķ√≥ŲĹŠĻŻ.
ĪĺŐ‚Ĺ‚őŲ£ļ
£®1£©”…![]() °őAB,Ķ√
°őAB,Ķ√![]() £¨°ŗt=6.
£¨°ŗt=6.
£®2£©…ŤACĪŖ…ŌĶńłŖő™h,”…![]() .
.
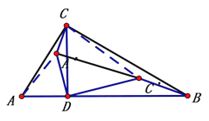
£®3£©ĘŔĶĪ6£ľt£ľ9 Ī£¨÷™600£ľ![]() £ľ900
£ľ900
»ÁÕľŃ¨Ĺ”AA°ģ°ĘC C°Į
”…–ż◊™∂®“Ś÷™
°ŌAD A°ģ=°ŌCD C°Į=°Ō![]()
°ŖAD=A°ģD°ĘCD= C°ģD
°ŗ°ųADA°ģ °◊°ųC D C°ģ£ģ
°ŗ°ŌA°ģA D =°ŌC°ģCD ; ![]() ,
,
”÷°Ŗ°ŌCAD =°ŌBCD =60O
°ŗ°ųACA°ģ °◊°ųC BC°Į
°ŗ![]() ő™∂®÷Ķ.
ő™∂®÷Ķ.
ĘŕĹŠ¬Ř≥…ŃĘ£¨Ī»÷Ķ»‘ő™![]() .
.
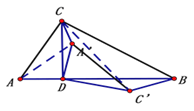



| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ2015ńÍ1‘¬£¨ –ĹŐ”żĺ÷‘ŕ»ę –÷––°—ß÷–—°»°Ńň63ňý—ß–£ī”—ß…ķĶńňľŌŽ∆∑Ķ¬°Ę—ß“Ķňģ∆Ĺ°Ę—ß“ĶłļĶ£°Ę…Ū–ń∑Ę’ĻļÕ–ň»§Őō≥§őŚłŲő¨∂»ĹÝ––Ńň◊ŘļŌ∆ņľŘ£ģ∆ņľŘ–°◊ť‘ŕ—°»°Ķńń≥÷–—ß∆ŖńÍľ∂»ęŐŚ—ß…ķ÷–ňśĽķ≥ť»°Ńň»Űł…√Ż—ß…ķĹÝ––ő ĺŪĶų≤ť£¨ŃňĹ‚ňŻ√«√ŅŐž‘ŕŅőÕ‚”√”ŕ—ßŌįĶń Īľš£¨≤ĘĽś÷∆≥…»ÁŌ¬≤ĽÕÍ’ŻĶńÕ≥ľ∆Õľ£ģ łýĺ›…Ō Ų–ŇŌĘ£¨Ĺ‚īūŌ¬Ń–ő Ő‚£ļ

£®1£©Īĺīő≥ť»°Ķń—ß…ķ»ň ż « ______ £Ľ…»–őÕ≥ľ∆Õľ÷–Ķń‘≤–ńĹ«¶ŃĶ»”ŕ ______ £Ľ≤Ļ»ęÕ≥ľ∆÷Ī∑ĹÕľ£Ľ
£®2£©ĪĽ≥ť»°Ķń—ß…ķĽĻ“™ĹÝ––“Ľīő50√◊Ň‹≤‚ ‘£¨√Ņ5»ň“Ľ◊ťĹÝ––£ģ‘ŕňśĽķ∑÷◊ť Ī£¨–°ļž°Ę–°Ľ®ŃĹ√ŻŇģ…ķĪĽ∑÷ĶĹÕ¨“ĽłŲ–°◊ť£¨«Ž”√Ń–ĪŪ∑®ĽÚĽ≠ ų◊īÕľ«ů≥ŲňżŃ©‘ŕ≥ťĶņīő Ī≥ť‘ŕŌŗŃŕŃĹĶņĶńłŇ¬ £ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°ŅŌ¬Ń–‘ňň„’ż»∑Ķń «£®°°°°£©
A.a2+a3£Ĺa2B.£®©Āa3£©2£Ĺa6
C.£®a©Āb£©2£Ĺa2©Āb2D.£®©Ā2a3£©2£Ĺ©Ā4a6
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™y+a”Žx+b£®a°Ębő™≥£ ż£©≥…’żĪ»ņż£ģ
£®1£©y «xĶń“ĽīőļĮ ż¬ū£Ņ«ŽňĶ√ųņŪ”…£Ľ
£®2£©‘ŕ ≤√īŐűľĢŌ¬y «xĶń’żĪ»ņżļĮ ż£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨AB «°—OĶń÷Īĺ∂£¨Ķ„P «y÷Š’żįŽ÷Š…ŌĶń“ĽĶ„£¨°—O”Žy÷Š’żįŽ÷ŠĹĽ”ŕĶ„C£¨PBĹĽ°—O”ŕĶ„D£¨Ķ„D «Ń”Ľ°![]() Ķń÷–Ķ„£¨AB=
Ķń÷–Ķ„£¨AB=![]() £ģ
£ģ
£®1£©«ů PĶ„Ķń◊ÝĪÍľį![]() Ķń÷Ķ£Ľ
Ķń÷Ķ£Ľ
£®2£©«ů÷§£ļDP2=OP°§CP.

≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»Ű“Ľ‘™∂Ģīő∑Ĺ≥Őax2=b£®ab£ĺ0£©ĶńŃĹłý∑÷Īūő™m+1”Ž2m©Ā4£ģ
£®1£©«ůmĶń÷Ķ£Ľ
£®2£©«ů ![]() Ķń÷Ķ£ģ
Ķń÷Ķ£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņő“Ļķőų≤ŅĶō«Ý‘ľ’ľő“ĻķĻķÕŃ√śĽżĶń![]() £¨ő“ĻķĻķÕŃ√śĽż‘ľ960ÕÚ∆Ĺ∑ĹĻęņÔ°£»Ű”√Ņ∆—ßľ« ż∑®ĪŪ ĺ£¨‘Úő“Ļķőų≤ŅĶō«ÝĶń√śĽżő™£®°°°°£©
£¨ő“ĻķĻķÕŃ√śĽż‘ľ960ÕÚ∆Ĺ∑ĹĻęņÔ°£»Ű”√Ņ∆—ßľ« ż∑®ĪŪ ĺ£¨‘Úő“Ļķőų≤ŅĶō«ÝĶń√śĽżő™£®°°°°£©
A. 6.4°Ń106∆Ĺ∑ĹĻęņÔ B. 6.4°Ń107∆Ĺ∑ĹĻęņÔ
C. 640°Ń104∆Ĺ∑ĹĻęņÔ D. 64°Ń105∆Ĺ∑ĹĻęņÔ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľňý ĺ£¨»ŰĹęņŗň∆”ŕa°Ęb°Ęc°ĘdňńłŲÕľĶńÕľ–ő≥∆◊Ų∆Ĺ√śÕľ£¨‘Ú∆š∂•Ķ„ ż°ĘĪŖ ż”Ž«Ý”Ú ż÷ģľšīś‘ŕń≥÷÷ĻōŌĶ£ģĻŘ≤žÕľbļÕĪŪ÷–∂‘”¶Ķń ż÷Ķ£¨ŐĹĺŅľ∆ żĶń∑Ĺ∑®≤Ę◊ųīū£ģ

£®1£© ż“Ľ ż√ŅłŲÕľ÷–łų”–∂ŗ…ŔłŲ∂•Ķ„°Ę∂ŗ…ŔŐűĪŖ£¨’‚–©ĪŖőß≥Ų∂ŗ…ŔłŲ«Ý”Ú≤ĘŐÓĪŪ£ļ
∆Ĺ√śÕľ | a | b | c | d |
∂•Ķ„ ż(S) | 7 | |||
ĪŖ ż(M) | 9 | |||
«Ý”Ú ż(N) | 3 |
£®2£©łýĺ›ĪŪ÷– ż÷Ķ£¨–ī≥Ų∆Ĺ√śÕľĶń∂•Ķ„ ż°ĘĪŖ ż°Ę«Ý”Ú ż÷ģľšĶń“Ľ÷÷ĻōŌĶő™ £Ľ
£®3£©»ÁĻŻ“ĽłŲ∆Ĺ√śÕľ”–20łŲ∂•Ķ„ļÕ11łŲ«Ý”Ú£¨ń«√īņŻ”√£®2£©÷–Ķ√≥ŲĶńĻōŌĶŅ…÷™’‚łŲ∆Ĺ√śÕľ”– ŐűĪŖ£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņį—∂ŗŌÓ Ĺa£≠4a∑÷Ĺ‚“Ú Ĺ£¨ĹŠĻŻ’ż»∑Ķń «°ĺ °Ņ
A.a (a-4) B. (a+2)(a-2) C. a(a+2)( a-2) D. (a£≠2 ) £≠4
≤ťŅīīūįłļÕĹ‚őŲ>>
Ļķľ —ß–£”Ň—° - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com