
【题目】一个二次函数图象上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | ﹣ | 0 |
| 2 |
| 0 | m | ﹣6 | ﹣ | … |
(1)求这个二次函数的表达式;
(2)求m的值;
(3)在给定的直角坐标系中,画出这个函数的图象;
(4)根据图象,写出当y<0时,x的取值范围.
【答案】(1)y=﹣![]() (x+1)2+2;(2)﹣
(x+1)2+2;(2)﹣![]() ;(3)详见解析;(4)y<0时,x<﹣3或x>1.
;(3)详见解析;(4)y<0时,x<﹣3或x>1.
【解析】
(1)先确定出顶点坐标,再设顶点式解析式为y=a(x+1)2+2,然后将点(1,0)代入求出a的值,从而得解;
(2)将x=2代入函数解析式计算即可得解;
(3)根据二次函数图象的画法作出图象即可;
(4)根据函数图象,写出x轴上方部分的x的取值范围即可.
(1)由图表可知抛物线的顶点坐标为(﹣1,2),
所以,设这个二次函数的表达式为y=a(x+1)2+2,
∵图象过点(1,0),
∴a(1+1)2+2=0,
∴a=﹣![]() ,
,
∴这个二次函数的表达式为y=﹣![]() (x+1)2+2;
(x+1)2+2;
(2)x=2时,m=﹣![]() (2+1)2+2=﹣
(2+1)2+2=﹣![]() ;
;
(3)函数图象如图所示;
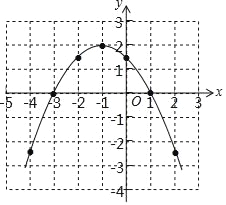
(4)y<0时,x<﹣3或x>1.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,要使△ABD≌△ACD,需从下列条件中增加一个,错误的选法是( )

A.∠ADB=∠ADCB.∠B=∠CC.AB=ACD.DB=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC和△DCE中,CA=CB,CD=CE,∠CAB= ∠CED=α.
(1)如图1,将AD、EB延长,延长线相交于点0.
①求证:BE= AD;
②用含α的式子表示∠AOB的度数(直接写出结果);
(2)如图2,当α=45°时,连接BD、AE,作CM⊥AE于M点,延长MC与BD交于点N.求证:N是BD的中点.
注:第(2)问的解答过程无需注明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
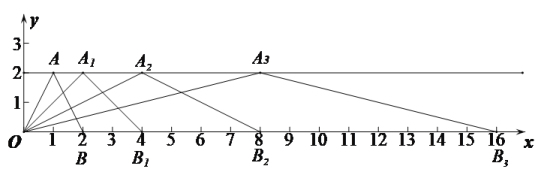
【题目】如下图所示,在直角坐标系中,第一次将△OAB变换成![]() ,第二次将
,第二次将![]() 变换成
变换成![]() ,第三次将
,第三次将![]() 变换成
变换成![]() ,已知
,已知![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)观察每次变换前后的三角形有何变化,找出规律,按此规律再将![]() 变换成
变换成![]() ,则
,则![]() 的坐标为 ,
的坐标为 ,![]() 的坐标为 .
的坐标为 .
(2)可以发现变换过程中![]() ……
……![]() 的纵坐标均为 .
的纵坐标均为 .
(3)按照上述规律将△OAB进行n次变换得到![]() ,则可知
,则可知![]() 的坐标为 ,
的坐标为 , ![]() 的坐标为 .
的坐标为 .
(4)线段![]() 的长度为 .
的长度为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
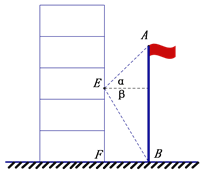
【题目】数学实践课上,同学们分组测量教学楼前国旗杆的高度.小泽同学所在的组先设计了测量方案,然后开始测量了.他们全组分成两个测量队,分别负责室内测量和室外测量(如图).室内测量组来到教室内窗台旁,在点E处测得旗杆顶部A的仰角α为45°,旗杆底部B的俯角β为60°. 室外测量组测得BF的长度为5米.则旗杆AB=______米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠ADC=90°,点E是BC边上一动点,联结AE,过点E作AE的垂线交直线CD于点F.已知AD=4cm,CD=2cm,BC=5cm,设BE的长为xcm,CF的长为ycm.
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行探究.
下面是小东的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 |
y/cm | 2.5 | 1.1 | 0 | 0.9 | 1.5 | 1.9 | 2 | 1.9 |
| 0.9 | 0 |
(说明:补全表格时相关数据保留一位小数)
(2)建立直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:当BE=CF时,BE的长度约为 cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,该店采取了降价措施.在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.
(1)若降价4元,则平均每天销售数量为 件;
(2)当每件商品降价多少元时,该商店每天销售利润为1050元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区为了绿化小区环境,建设和谐家园,准备将一块周长为76米的长方形空地,设计成长和宽分别相等的9块小长方形,如图所示,计划在空地上种上各种花卉,经市场预测,绿化每平方米空地造价210元,请计算,要完成这块绿化工程,预计花费多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD和AEFG是两个互相重合的矩形,如图2将矩形AEFG绕点A按顺时针方向旋转α度(0≤α≤90°),点G恰好落在矩形ABCD的对角线上,AB与FG相交于点M,连接BE交FG于点N.
(1)当AB=AD时,请直接写出∠ABE的度数;
(2)当∠ADB=60°时,求∠ABE的度数;
(3)如图3,当AB=2AD=2时,①求点A到直线BE的距离; ②直接写出△BMN的周长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com