

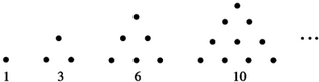
分析 结合图形发现规律“从第二个图形开始,每个图形中黑色三角形的个数都是前一个图形的3倍”,结合a1=1即可得出a2015的值,从而得出结论.
解答 解:观察图形发现:从第二个图形开始,每个图形中黑色三角形的个数都是前一个图形的3倍,
∴有a1=1,a2=3,a3=9,a4=27,…,${a}_{n}={3}^{(n-1)}$.
令n=2015可得:a2015=3(2015-1)=32014.
故答案为:32014.
点评 本题考查了图形的变化类,解题的关键是找出“从第二个图形开始,每个图形中黑色三角形的个数都是前一个图形的3倍”这一规律.本题属于基础题,难度不大,解决该题型题目时,根据图形的变化找出变化规律是关键.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 有一个实数根 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com