
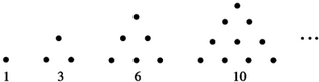
分析 研究图形发现规律“第n个“三角形数”是1+2+…+n=$\frac{n(n+1)}{2}$”,代入n=50即可得出结论.
解答 解:观察图形,发现第1个“三角形数”是1,第2个是1+2=3,第3个是1+2+3=6,第4个是1+2+3+4=10,…
由此发现规律:第n个“三角形数”是1+2+…+n=$\frac{n(n+1)}{2}$.
第50个“三角形数”是1+2+…+49+50=$\frac{50×(50+1)}{2}$=1275.
故答案为:1275.
点评 本题考查了图形的变化规律,解题关键是找出“第n个“三角形数”是1+2+…+n=$\frac{n(n+1)}{2}$”这一规律.本题属于基础题,难度不大,解决该题型题目时,分析图形得出规律是关键.


科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com