
分析 由题意可得,第n+1周也使用A种密码的概率 Pn+1=Pn•$\frac{1}{3}$,且P2=0,P3=$\frac{1}{3}$,以此类推可得第七周使用A的概率P7 的值.
解答 解:第一周使用A,第二周使用A的概率P2=0,第三周使用A的概率P3=$\frac{1}{3}$,依此类推,
第四周使用A的概率 P4=(1-$\frac{1}{3}$)•$\frac{1}{3}$=$\frac{2}{9}$,
第五周使用A的概率P5=(1-$\frac{2}{9}$)•$\frac{1}{3}$=$\frac{7}{27}$,
第六周使用A的概率P6=(1-P5)•$\frac{1}{3}$=$\frac{20}{81}$,
第七周使用A的概率P7=(1-P6)•$\frac{1}{3}$=$\frac{61}{243}$;
故答案为:$\frac{61}{243}$.
点评 此题主要考查了概率公式,得到第n+1周也使用A种密码的概率 Pn+1=Pn•$\frac{1}{3}$,是解题的关键,属于中档题.


科目:初中数学 来源: 题型:解答题
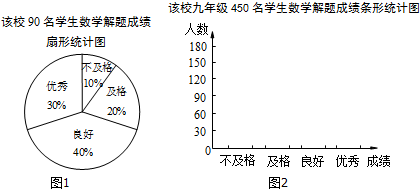
| 成绩 | 划记 | 频数 |
| 不及格 | 正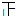 | 9 |
| 及格 | 正正正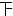 | 18 |
| 良好 | 正正正正正正一 | 36 |
| 优秀 | 正正正正正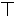 | 27 |
| 合计 | 90 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com