
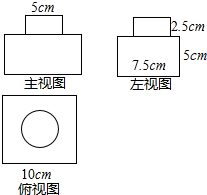
 如图是一个铁制零件的三视图及尺寸标注.
如图是一个铁制零件的三视图及尺寸标注.分析 (1)结合三视图可知该几何体是长方体与圆柱的组合体;
(2)由(1)知其表面积为长方体面积+圆柱的侧面积,列式计算可得.
解答 解:(1)该几何体是长为10cm、宽为7.5cm、高为5cm的长方体上放一个直径为5cm、高为2.5cm的圆柱体的组合体;
(2)顶面积=长×宽=10×7.5=75(cm2),
底面积=长×宽=10×7.5=75(cm2),
侧面积=长×高×2+宽×高×2+π×直径×高
=10×7.5×2+7.5×5×2+π×5×2.5
≈150+75+39.25≈264.25(cm2),
故表面积=75+75+264.25=414.25(cm2).
点评 考查了由三视图判断几何体,由三视图想象几何体的形状,首先应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,然后综合起来考虑整体形状.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
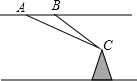 如图,飞机的飞行高度为2500米,在A点处测得某电视塔尖点C的俯角为30°,保持方向不变前进1200米到达B点时测得该电视塔尖点C的俯角为45°.请计算电视塔的高度(结果保留整数,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,飞机的飞行高度为2500米,在A点处测得某电视塔尖点C的俯角为30°,保持方向不变前进1200米到达B点时测得该电视塔尖点C的俯角为45°.请计算电视塔的高度(结果保留整数,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
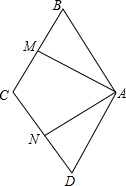 已知:如图,在菱形ABCD中,∠BAD=120°,点M,N分别在BC和CD上,且∠MAN=60°.
已知:如图,在菱形ABCD中,∠BAD=120°,点M,N分别在BC和CD上,且∠MAN=60°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=ax2+bx+c与y轴交于A点,过点A的直线y=$\frac{1}{2}$x+1与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0),又抛物线的对称轴为x=$\frac{17}{10}$.
如图,抛物线y=ax2+bx+c与y轴交于A点,过点A的直线y=$\frac{1}{2}$x+1与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0),又抛物线的对称轴为x=$\frac{17}{10}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com