
 ��ͼ��������y=ax2+bx+c��y�ύ��A�㣬����A��ֱ��y=$\frac{1}{2}$x+1�������߽�����һ��B������B��BC��x�ᣬ����Ϊ��C��3��0�����������ߵĶԳ���Ϊx=$\frac{17}{10}$��
��ͼ��������y=ax2+bx+c��y�ύ��A�㣬����A��ֱ��y=$\frac{1}{2}$x+1�������߽�����һ��B������B��BC��x�ᣬ����Ϊ��C��3��0�����������ߵĶԳ���Ϊx=$\frac{17}{10}$������ ��1�����ݴ���ϵ�������ɵú�������ʽ��
��2������ƽ����y���ֱ���������ľ����ǽϴ�����������С�������꣬�ɵô𰸣�
��3������ƽ���ı��εĶԱ���ȣ��ɵù���t�ķ��̣����ݽⷽ�̣��ɵô𰸣��������ε��ڱ���ȣ��ɵô𰸣�
��� ��1�������⣬��A��0��1����B��3��$\frac{3}{2}$�����������ߵĶԳ���Ϊx=$\frac{17}{10}$����
$\left\{\begin{array}{l}{c=1}\\{9a+3b+c=\frac{3}{2}}\\{-\frac{b}{2a}=\frac{17}{10}}\end{array}\right.$�����$\left\{\begin{array}{l}{a=-\frac{5}{4}}\\{b=\frac{17}{4}}\\{c=1}\end{array}\right.$��
���������ߵĺ�����ϵʽΪy=-$\frac{5}{4}$x2+$\frac{17}{4}$x+1��
��2��������֪OP=t����P��t��0����M��t��$\frac{1}{2}$t+1����N��t��-$\frac{5}{4}$t2+$\frac{17}{4}$t+1����
����s=MN=NP-MP=-$\frac{5}{4}$t2+$\frac{17}{4}$t+1-��$\frac{1}{2}$t+1��=-$\frac{5}{4}$t2+$\frac{15}{4}$t��
����t��ȡֵ��Χ��0��t��3��
��s��t�ĺ�����ϵʽs=-$\frac{5}{4}$t2+$\frac{15}{4}$t��0��t��3����
��3�����ı���BCMNΪƽ���ı��Σ�����MN=BC����ʱ��-$\frac{5}{4}$t2+$\frac{15}{4}$t=$\frac{5}{2}$�����t1=1��t2=2��
���Ե�t=1��t=2ʱ���ı���BCMNΪƽ���ı��Σ�
��t=1ʱ��ƽ���ı���BCMN�����Σ���t=2ʱ��ƽ���ı���BCMN�������Σ��������£�
�ٵ�t=1ʱ��P��1��0����M��1��$\frac{3}{2}$����N��1��4��������MP=$\frac{3}{2}$��NP=4����MN=NP-MP=$\frac{5}{2}$��
����Rt��MPC��MC=$\sqrt{M{P}^{2}+P{C}^{2}}$=$\frac{5}{2}$������MN=MC��
��ʱƽ���ı���BCMN�����Σ�
�ڵ�t=2ʱ��MP=2��NP=$\frac{9}{2}$����MN=NP-MP=$\frac{5}{2}$��
����Rt��MPC��MC=$\sqrt{M{P}^{2}+P{C}^{2}}$=$\sqrt{5}$������MN��MC��
��ʱƽ���ı���BCMN�������Σ�
���� ���⿼���˶��κ����ۺ��⣬���ô���ϵ������������ʽ������ƽ���ı��εĶԱ���ȵó�����t�ķ����ǽ���ؼ����������ε��ڱ�����ǽ���ؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
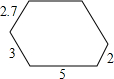 ��ͼ��һ�������ε�ÿ���ڽǶ���120�㣬�����ıߵij�������2.7��3��5��2����������ε��ܳ���20.7��
��ͼ��һ�������ε�ÿ���ڽǶ���120�㣬�����ıߵij�������2.7��3��5��2����������ε��ܳ���20.7���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
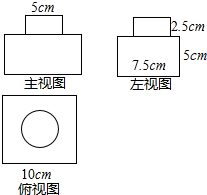 ��ͼ��һ���������������ͼ���ߴ��ע��
��ͼ��һ���������������ͼ���ߴ��ע���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 100��1+x��=123 | B�� | 100��1-x��=123 | C�� | 100��1+x��2=123 | D�� | 100��1-x��2=123 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
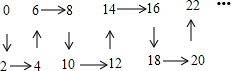
| A�� | ���� | B�� | ���� | C�� | ���� | D�� | ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{10}$ | B�� | $\frac{3}{10}$ | C�� | $\frac{2}{5}$ | D�� | $\frac{1}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �٢ڢۢܢ� | B�� | �ۢݢ� | C�� | �٢ڢ� | D�� | �ܢ� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com