
 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=35°,则∠B的度数是( )
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=35°,则∠B的度数是( )| A. | 80° | B. | 75° | C. | 70° | D. | 65° |
分析 根据旋转的性质可得AC=A′C,然后判断出△ACA′是等腰直角三角形,根据等腰直角三角形的性质可得∠CAA′=45°,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠A′B′C,然后根据旋转的性质可得∠B=∠A′B′C.
解答 解:∵Rt△ABC绕直角顶点C顺时针旋转90°得到△A′B′C,
∴AC=A′C,
∴△ACA′是等腰直角三角形,
∴∠CAA′=45°,
∴∠A′B′C=∠1+∠CAA′=35°+45°=80°,
由旋转的性质得∠B=∠A′B′C=80°.
故选:A.
点评 本题考查了旋转的性质,等腰直角三角形的判定与性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质并准确识图是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
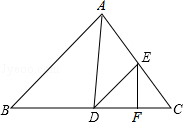 如图,在△ABC中,∠B=54°,AD平分∠CAB,交BC于D,E为AC边上一点,连结DE,∠EAD=∠EDA,EF⊥BC于点F.求∠FED的度数.
如图,在△ABC中,∠B=54°,AD平分∠CAB,交BC于D,E为AC边上一点,连结DE,∠EAD=∠EDA,EF⊥BC于点F.求∠FED的度数.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
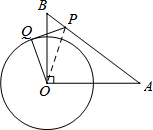 如图,在Rt△OAB中,∠AOB=90°,OA=4,OB=3.⊙O的半径为2,点P是线段AB上的一动点,过点P作⊙O的一条切线PQ,Q为切点.设AP=x,PQ2=y,则y与x的函数图象大致是( )
如图,在Rt△OAB中,∠AOB=90°,OA=4,OB=3.⊙O的半径为2,点P是线段AB上的一动点,过点P作⊙O的一条切线PQ,Q为切点.设AP=x,PQ2=y,则y与x的函数图象大致是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
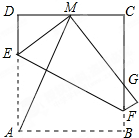 将边长为5正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G.
将边长为5正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | ②③④ | B. | ①②③ | C. | ①③④ | D. | ①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
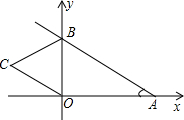 如图,直线y=kx+4与x,y轴分别交于A,B两点,以OB为边在y轴左侧作等边三角形OBC,将△OBCB沿y轴翻折后,点C的对应点C′恰好落在直线AB上,则k的值为-$\frac{\sqrt{3}}{3}$.
如图,直线y=kx+4与x,y轴分别交于A,B两点,以OB为边在y轴左侧作等边三角形OBC,将△OBCB沿y轴翻折后,点C的对应点C′恰好落在直线AB上,则k的值为-$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
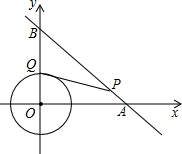 如图,⊙O是以原点为圆心,$\sqrt{2}$为半径的圆,点P是直线y=-x+6上的一点,过点P 作⊙O的一条切线PQ,Q为切点,则△OPQ面积的最小值为2$\sqrt{2}$.
如图,⊙O是以原点为圆心,$\sqrt{2}$为半径的圆,点P是直线y=-x+6上的一点,过点P 作⊙O的一条切线PQ,Q为切点,则△OPQ面积的最小值为2$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
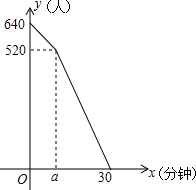 汛期来临,水库水位不断上涨,经勘测发现,水库现在超过警戒线水量640万米3,设水流入水库的速度是固定的,每个泄洪闸速度也是固定的,泄洪时,每小时流入水库的水量16万米3,每小时每个泄洪闸泄洪14万米3,已知泄洪的前a小时只打开了两个泄洪闸,水库超过警戒线的水量y(万米3)与泄洪时间s(小时)的关系如图所示,根据图象解答问题:
汛期来临,水库水位不断上涨,经勘测发现,水库现在超过警戒线水量640万米3,设水流入水库的速度是固定的,每个泄洪闸速度也是固定的,泄洪时,每小时流入水库的水量16万米3,每小时每个泄洪闸泄洪14万米3,已知泄洪的前a小时只打开了两个泄洪闸,水库超过警戒线的水量y(万米3)与泄洪时间s(小时)的关系如图所示,根据图象解答问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com