
【题目】将抛物线y=3x2向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为( )
A.y=3 ![]() +3
+3
B.y=3 ![]() +3
+3
C.y=3 ![]() -3
-3
D.y=3 ![]() -3
-3
科目:初中数学 来源: 题型:
【题目】如图,在五边形 ABCDE 中,∠A+∠B+∠E=α,DP,CP 分别平分∠EDC,∠BCD,则∠P 的度数是( )

A. 90°+![]() α B.
α B. ![]() α﹣90° C.
α﹣90° C. ![]() α D. 540° -
α D. 540° -![]() α
α
查看答案和解析>>
科目:初中数学 来源: 题型:
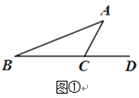
【题目】感知:如图①,∠ACD为△ABC的外角,易得∠ACD=∠A+∠B(不需证明) ;
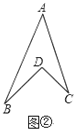
探究:如图②,在四边形ABDC中,试探究∠BDC与∠A、∠B.、∠C之间的关系,并说明理由;
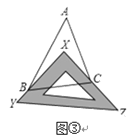
应用:如图③,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=50°,则∠ABX+∠ACX=_______度;(直接填答案,不需证明)
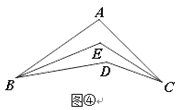
拓展:如图④,BE平分∠ABD,CE平分∠ACD,若∠BAC=100°,∠BDC=150°,则∠BEC=_______度. (直接填答案,不需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好改善河流的水质,治污公司决定购买10台污水处理设备.现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
A型 | B型 | |
价格(万元/台) | a | b |
处理污水量(吨/月) | 240 | 180 |
(1)求a,b的值;
(2)治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点, ![]() 的圆心坐标为
的圆心坐标为![]() ,半径为
,半径为![]() 函数
函数![]() 的图象与x轴交于点A,与y轴交于点B,点P为线段AB上一动点.
的图象与x轴交于点A,与y轴交于点B,点P为线段AB上一动点.
![]() 连接CO,求证:
连接CO,求证: ![]() ;
;
![]() 若
若![]() 是等腰三角形,求点P的坐标;
是等腰三角形,求点P的坐标;
![]() 当直线PO与
当直线PO与![]() 相切时,求
相切时,求![]() 的度数;当直线PO与
的度数;当直线PO与![]() 相交时,设交点为E、F,点M为线段EF的中点,令
相交时,设交点为E、F,点M为线段EF的中点,令![]() ,求s与t之间的函数关系,并写出t的取值范围.
,求s与t之间的函数关系,并写出t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,阴影部分是边长为a的大正方形中剪去一个边长为b的小正方形后所得到的图形,将阴影部分通过割、拼,形成新的图形,给出下列3种割拼方法,其中能够验证平方差公式的是( )

A. ①② B. ②③ C. ①③ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接“五一劳动节”,某超市开展促销活动,决定对A,B两种商品进行打折出售.打折前,买6件A商品和3件B商品需要108元,买3件A商品和4件B商品需要94元.问:打折后,若买5件A商品和4件B商品仅需86元,比打折前节省了多少元钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,八一广场要设计一个矩形花坛,花坛的长、宽分别为200m、120m,花坛中有一横两纵的通道,横、纵通道的宽度分别为3xm、2xm.
(1)用代数式表示三条通道的总面积S;当通道总面积为花坛总面积的 ![]() 时,求横、纵通道的宽分别是多少?
时,求横、纵通道的宽分别是多少?
(2)如果花坛绿化造价为每平方米3元,通道总造价为3168x元,那么横、纵通道的宽分别为多少米时,花坛总造价最低?并求出最低造价.(以下数据可供参考:852=7225,862=7396,872=7569)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】证明题
(1)已知一元二次方程x2+px+q=0(p2-4q≥0)的两根为x1、x2;求证:x1+x2=-p , x1 x2=q .
(2)已知抛物线y=x2+px+q与x轴交于A、B两点,且过点(-1,-1),设线段AB的长为d,当p为何值时,d2取得最小值,并求出最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com