
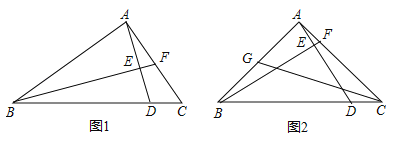
【题目】如图,直角△ABC中,∠BAC=90°,D在BC上,连接AD,作BF⊥AD分别交AD于E,AC于F.
(1)如图1,若BD=BA,求证:△ABE≌△DBE;
(2)如图2,若BD=4DC,取AB的中点G,连接CG交AD于M,求证:①GM=2MC;②AG2=AFAC.
【答案】(1)证明见解析;(2)①证明见解析;②证明见解析.
【解析】
试题分析:(1)根据全等三角形的判定定理即可得到结论;
(2)①过G作GH∥AD交BC于H,由AG=BG,得到BH=DH,根据已知条件设DC=1,BD=4,得到BH=DH=2,根据平行线分线段成比例定理得到![]() ,求得GM=2MC;
,求得GM=2MC;
②过C作CN⊥AD交AD的延长线于N,则CN∥AG,根据相似三角形的性质得到![]() ,由①知GM=2MC,得到2NC=AG,根据相似三角形的性质得到
,由①知GM=2MC,得到2NC=AG,根据相似三角形的性质得到![]() ,等量代换得到
,等量代换得到![]() ,于是得到结论.
,于是得到结论.
试题解析:(1)在Rt△ABE和Rt△DBE中,∵BA=BD,BE=BE,∴△ABE≌△DBE;
(2)①过G作GH∥AD交BC于H,∵AG=BG,∴BH=DH,∵BD=4DC,设DC=1,BD=4,∴BH=DH=2,∵GH∥AD,∴![]() ,∴GM=2MC;
,∴GM=2MC;
②过C作CN⊥AC交AD的延长线于N,则CN∥AG,∴△AGM∽△NCM,∴![]() ,由①知GM=2MC,∴2NC=AG,∵∠BAC=∠AEB=90°,∴∠ABF=∠CAN=90°﹣∠BAE,∴△ACN∽△BAF,∴
,由①知GM=2MC,∴2NC=AG,∵∠BAC=∠AEB=90°,∴∠ABF=∠CAN=90°﹣∠BAE,∴△ACN∽△BAF,∴![]() ,∵AB=AG,∴
,∵AB=AG,∴![]() ,∴2CNAG=AFAC,∴AG2=AFAC.
,∴2CNAG=AFAC,∴AG2=AFAC.


科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.“任意画出一个等边三角形,它是轴对称图形”是随机事件
B.“任意画出一个平行四边形,它是中心对称图形”是必然事件
C.“概率为0.0001的事件”是不可能事件
D.任意掷一枚质地均匀的硬币10次,正面向上的一定是5次
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,规定:抛物线
中,规定:抛物线![]() 的伴随直线为
的伴随直线为![]() .例如:抛物线
.例如:抛物线![]() 的伴随直线为
的伴随直线为![]() ,即
,即![]()
(1)在上面规定下,抛物线![]() 的顶点为 .伴随直线为 ;抛物线
的顶点为 .伴随直线为 ;抛物线![]() 与其伴随直线的交点坐标为 和 ;
与其伴随直线的交点坐标为 和 ;
(2)如图,顶点在第一象限的抛物线![]() 与其伴随直线相交于点
与其伴随直线相交于点![]() (点
(点![]() 在点
在点![]() 的右侧)与
的右侧)与![]() 轴交于点
轴交于点![]()
①若![]() 求
求![]() 的值;
的值;
②如果点![]() 是直线
是直线![]() 上方抛物线的一个动点,
上方抛物线的一个动点,![]() 的面积记为
的面积记为![]() ,当
,当![]() 取得最大值
取得最大值![]() 时,求
时,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB,
(1)求证:四边形AEBD是菱形;
(2)如果OA=3,OC=2,求出经过点E的反比例函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市今年约有140000人报名参加初中学业水平考试,用科学记数法表示140000为( )
A.14×104
B.14×103
C.1.4×104
D.1.4×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P位于第二象限,距y轴3个单位长度,距x轴4个单位长度,则点P的坐标是( )
A. (-3,4)B. (3,-4)C. (4,-3)D. (-4,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=BC , ∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF . 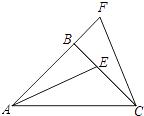
(1)求证:△ABE≌△CBF;
(2)若∠BAE=25°,求∠ACF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
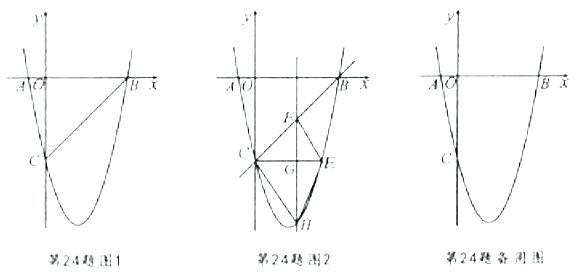
【题目】如图1,在平面直角坐标系中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线的函数表达式;
(2)若点![]() 是
是![]() 轴上的一点,且以
轴上的一点,且以![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点
相似,求点![]() 的坐标;
的坐标;
(3)如图2,![]() 轴玮抛物线相交于点
轴玮抛物线相交于点![]() ,点
,点![]() 是直线
是直线![]() 下方抛物线上的动点,过点
下方抛物线上的动点,过点![]() 且与
且与![]() 轴平行的直线与
轴平行的直线与![]() ,
,![]() 分别交于点
分别交于点![]() ,
,![]() ,试探究当点
,试探究当点![]() 运动到何处时,四边形
运动到何处时,四边形![]() 的面积最大,求点
的面积最大,求点![]() 的坐标及最大面积;
的坐标及最大面积;
(4)若点![]() 为抛物线的顶点,点
为抛物线的顶点,点![]() 是该抛物线上的一点,在
是该抛物线上的一点,在![]() 轴,
轴,![]() 轴上分别找点
轴上分别找点![]() ,
,![]() ,使四边形
,使四边形![]() 的周长最小,求出点
的周长最小,求出点![]() ,
,![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com