
【题目】如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB,
(1)求证:四边形AEBD是菱形;
(2)如果OA=3,OC=2,求出经过点E的反比例函数解析式.
【答案】
(1)证明:∵BE∥AC,AE∥OB,
∴四边形AEBD是平行四边形,
∵四边形OABC是矩形,
∴DA= ![]() AC,DB=
AC,DB= ![]() OB,AC=OB,AB=OC=2,
OB,AC=OB,AB=OC=2,
∴DA=DB,
∴四边形AEBD是菱形;
(2)解:连接DE,交AB于F,如图所示:

∵四边形AEBD是菱形,
∴AB与DE互相垂直平分,
∵OA=3,OC=2,
∴EF=DF= ![]() OA=
OA= ![]() ,AF=
,AF= ![]() AB=1,3+
AB=1,3+ ![]() =
= ![]() ,
,
∴点E坐标为:( ![]() ,1),
,1),
设经过点E的反比例函数解析式为:y= ![]() ,
,
把点E( ![]() ,1)代入得:k=
,1)代入得:k= ![]() ,
,
∴经过点E的反比例函数解析式为:y= ![]() .
.
【解析】(1)根据矩形的性质对角线相等且互相平分,得到DA=DB,由平行四边形的定义得到四边形AEBD是平行四边形,在根据菱形的定义得到四边形AEBD是菱形;(2)根据菱形的性质对角线互相垂直平分,得到EF=DF、AF的值,得到点E的坐标,求出经过点E的反比例函数解析式.
【考点精析】根据题目的已知条件,利用矩形的性质的相关知识可以得到问题的答案,需要掌握矩形的四个角都是直角,矩形的对角线相等.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】某班组织20名同学去春游,同时租用两种型号的车辆,一种车每辆有8个座位,另一种车每辆有4个座位,要求租用的车辆不留空座,也不能超载.租车方案共有( )种.
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
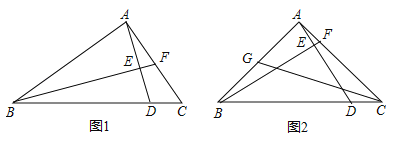
【题目】如图,直角△ABC中,∠BAC=90°,D在BC上,连接AD,作BF⊥AD分别交AD于E,AC于F.
(1)如图1,若BD=BA,求证:△ABE≌△DBE;
(2)如图2,若BD=4DC,取AB的中点G,连接CG交AD于M,求证:①GM=2MC;②AG2=AFAC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC内一点P满足PA=PB=PC,则点P一定是△ABC的( )
A. 三边垂直平分线的交点 B. 三条内角平分线的交点
C. 三条高的交点 D. 三条中线的交点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com