
科目:初中数学 来源: 题型:
 |
| BD |
 |
| BD |
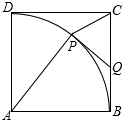 △CPQ进行研究.
△CPQ进行研究.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(贵州贵阳卷)数学(解析版) 题型:解答题
在△ABC中,BC=a,AC=b,AB=c,设c为最长边,当a2+b2=c2时,△ABC是直角三角形;当a2+b2≠c2时,利用代数式a2+b2和c2的大小关系,探究△ABC的形状(按角分类).
(1)当△ABC三边分别为6、8、9时,△ABC为 三角形;当△ABC三边分别为6、8、11时,△ABC为 三角形.
(2)猜想,当a2+b2 c2时,△ABC为锐角三角形;当a2+b2 c2时,△ABC为钝角三角形.
(3)判断当a=2,b=4时,△ABC的形状,并求出对应的c的取值范围.
查看答案和解析>>
科目:初中数学 来源:湖北省中考真题 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:
在-次数学活动课上,老师出了-道题:
(1)解方程x2-2x-3=0.
巡视后老师发现同学们解此题的方法有公式法、配方法和十字相乘法(分解因式法)。
接着,老师请大家用自己熟悉的方法解第二道题:
(2)解关于x的方程mx2+(m一3)x一3=0(m为常数,且m≠0).
老师继续巡视,及时观察、点拨大家.再接着,老师将第二道题变式为第三道题:
(3)已知关于x的函数y=mx2+(m-3)x-3(m为常数).
①求证:不论m为何值,此函数的图象恒过x轴、y轴上的两个定点(设x轴上的定点为A,y轴上的定点为C);
②若m≠0时,设此函数的图象与x轴的另一个交点为反B,当△ABC为锐角三角形时,求m的取值范围;当△ABC为钝角三角形时,观察图象,直接写出m的取值范围.
请你也用自己熟悉的方法解上述三道题.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com