
【题目】如图,在平面直角坐标系中,反比例函数y= ![]() (x>0)的图象上有一点A(m,4),过点A作AB⊥x轴于点B,将点B向右平移2个单位长度得到点C,过点C作y轴的平行线交反比例函数的图象于点D,CD=
(x>0)的图象上有一点A(m,4),过点A作AB⊥x轴于点B,将点B向右平移2个单位长度得到点C,过点C作y轴的平行线交反比例函数的图象于点D,CD= ![]()
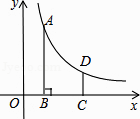
(1)点D的横坐标为(用含m的式子表示);
(2)求反比例函数的解析式.
科目:初中数学 来源: 题型:
【题目】甲、乙两人5次射击命中的环数如下:
甲 | 7 | 9 | 8 | 6 | 10 |
乙 | 7 | 8 | 9 | 8 | 8 |
则以下判断中正确的是( )
A.![]() 甲=
甲= ![]() 乙 , S甲2=S乙2 .
乙 , S甲2=S乙2 .
B.![]() 甲=
甲= ![]() 乙 , S甲2>S乙2 .
乙 , S甲2>S乙2 .
C.![]() 甲=
甲= ![]() 乙 , S甲2<S乙2 .
乙 , S甲2<S乙2 .
D.![]() 甲<
甲< ![]() 乙 , S甲2<S乙2 .
乙 , S甲2<S乙2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:德国著名数学家高斯被认为是历史上最重要的数学家之一,并有"数学王子"的美誉.高斯从小就善于观察和思考.在他读小学时候就能在课堂上快速的计算出![]() ,今天我们可以将高斯的做法归纳如下:
,今天我们可以将高斯的做法归纳如下:
令![]() ①
①
![]() ②
②
(右边相加100+1=2+99=3+98=…..=100+1共100组)
①+②:有2S=101x100 解得:![]()
(1)请参照以上做法,回答,3+5+7+9+…..+97= ;
请尝试解决下列问题:
如下图,有一个形如六边形的点阵,它的中心是一个点,算第一层,第二层每边有两个点,第三层每边有三个点,依此类推.

(2)填写下表:
层数 | 1 | 2 | 3 | 4 |
该层对应的点数 | 1 | 6 | 12 | 18 |
所有层的总点数的和 | 1 | 7 | 19 |
①写出第n层所对应的点数;(n≥2)
②如果某一层共96个点,求它是第几层;
③写出n层的六边形点阵的总点数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在AB上,点M、N分别是AC、BC的中点,
(1)若AC=12cm,BC=10cm,求线段MN的长;
(2)若点C为线段AB上任意一点,满足AC+BC=acm,其它条件不变,你能猜想MN的长度吗?并说明理由;
(3)若点C在线段AB的延长线上,且满足AC-BC=bcm,点M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,并说明理由.请用一句简洁的话描述你发现的结论.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B都在数轴上,O为原点.
(1)点B表示的数是_________________;
(2)若点B以每秒2个单位长度的速度沿数轴向右运动,则2秒后点B表示的数是________;
(3)若点A、B分别以每秒1个单位长度、3个单位长度的速度沿数轴向右运动,而点O不动,t秒后,A、B、O三个点中有一个点是另外两个点为端点的线段的中点,求t的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着我市社会经济的发展和交通状况的改善,我市的旅游业得到了高速发展![]() 某旅游公司对我市一企业个人旅游年消费情况进行问卷调查
某旅游公司对我市一企业个人旅游年消费情况进行问卷调查![]() 随机抽取部分员工,记录每个人年消费金额,并将调查数据适当整理,绘制成如下两幅尚不完整的表和图:
随机抽取部分员工,记录每个人年消费金额,并将调查数据适当整理,绘制成如下两幅尚不完整的表和图:
组别 | 个人年消费金额 | 频数 | 频率 |
A |
| 18 |
|
B |
| a | b |
C |
|
|
|
D |
| 24 |
|
E |
| 12 |
|
合计 | c |
| |

根据以上信息解答下列问题:
![]() ________;
________; ![]() ________;
________; ![]() ________;
________;
![]() 补全频数分布直方图;
补全频数分布直方图;
![]() 若这个企业有3000名员工,请你估计个人旅游年消费金额在6000元以上的人数.
若这个企业有3000名员工,请你估计个人旅游年消费金额在6000元以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y1=﹣x2+4x和直线y2=2x.我们约定:当x任取一值时,x对应的函数值分别为y1、y2 , 若y1≠y2 , 取y1、y2中的较小值记为M;若y1=y2 , 记M=y1=y2 . 下列判断: ①当x>2时,M=y2;
②当x<0时,x值越大,M值越大;
③使得M大于4的x值不存在;
④若M=2,则x=1.
其中正确的有( )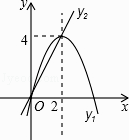
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为深化义务教育课程改革,满足学生的个性化学习需求,某校就“学生对知识拓展,体育特长、艺术特长和实践活动四类选课意向”进行了抽样调查(每人选报一类),绘制了如图所示的两幅统计图(不完整),请根据图中信息,解答下列问题: 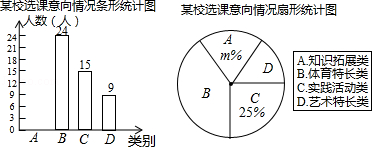
(1)求扇形统计图中m的值,并补全条形统计图;
(2)在被调查的学生中,随机抽一人,抽到选“体育特长类”或“艺术特长类”的学生的概率是多少?
(3)已知该校有800名学生,计划开设“实践活动类”课程每班安排20人,问学校开设多少个“实践活动类”课程的班级比较合理?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com