
【题目】如图![]() ,点C为△ABD外接圆上的一动点(点C不在
,点C为△ABD外接圆上的一动点(点C不在![]() 上,且不与点B,D重合),∠ACB=∠ABD=45°.
上,且不与点B,D重合),∠ACB=∠ABD=45°.
(1)求证:BD是该外接圆的直径;
(2)连结CD,求证:![]() AC=BC+CD;
AC=BC+CD;
(3)若△ABC关于直线AB的对称图形为△ABM,连接DM,试探究![]() ,
,![]() 三者之间满足的等量关系,并证明你的结论.
三者之间满足的等量关系,并证明你的结论.

【答案】(1)详见解析;(2)详见解析;(3)DM2=BM2+2MA2,理由详见解析.
【解析】
试题分析:(1)易证△ABD为等腰直角三角形,即可判定BD是该外接圆的直径;(2)如图所示作CA⊥AE,延长CB交AE于点E,再证△ACE为等腰直角三角形,可得AC=AE,再由勾股定理即可得![]() ;利用SAS判定△ABE≌△ADC,可得BE=DC,所以CE=BE+B,所以C=DC+BC=
;利用SAS判定△ABE≌△ADC,可得BE=DC,所以CE=BE+B,所以C=DC+BC=![]() ;(3)延长MB交圆于点E,连结AE、DE,因∠BEA=∠ACB=∠BMA=45°,在△MAE中有MA=AE,∠MAE=90°,由勾股定理可得
;(3)延长MB交圆于点E,连结AE、DE,因∠BEA=∠ACB=∠BMA=45°,在△MAE中有MA=AE,∠MAE=90°,由勾股定理可得![]() ,再证∠BED=90°,在RT△MED中,有
,再证∠BED=90°,在RT△MED中,有![]() ,所以
,所以![]() .
.
试题解析:(1)∵弧AB=弧AB, ∴∠ADB=∠ACB
又∵∠ACB=∠ABD=45° ∴∠ABD=∠ADB=45°
∴∠BAD=90° ∴△ABD为等腰直角三角形
∴BD是该外接圆的直径
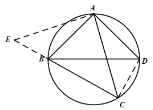
(2)如图所示作CA⊥AE,延长CB交AE于点E
∵∠ACB=45°,CA⊥AE
∴△ACE为等腰直角三角形 ∴AC=AE
由勾股定理可知CE2=AC2+AE2=2AC2 ∴![]()
由(1)可知△ABD 为等腰直角三角形
∴AB=AD ∠BAD=90° 又∵∠EAC=90°
∴∠EAB+∠BAC=∠DAC+∠BAC ∴∠EAB=∠DAC
∴在△ABE和△ADC中
∴△ABE≌△ADC(SAS)
∴BE=DC
∴CE=BE+BC=DC+BC=![]()
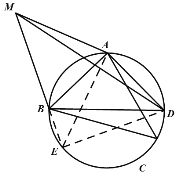
(3)DM2=BM2+2MA2
延长MB交圆于点E,连结AE、DE
∵∠BEA=∠ACB=∠BMA=45°
∴在△MAE中有MA=AE,∠MAE=90°
∴![]()
又∵AC=MA=AE
∴![]() =
=![]()
又∵![]() =
=![]()
∴![]() -
-![]() +
+![]() =
=![]() -
-![]() +
+![]()
即![]() =
=![]()
∴DE=BC=MB
∵BD为直径
∴∠BED=90°
在RT△MED中,有![]()
∴![]()



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c (a≠0)的图像与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC. 则下列结论:
①abc>0 ②9a+3b+c<0 ③c>-1 ④关于x的方程ax2+bx+c=0 (a≠0)有一个根为-![]()
其中正确的结论个数有( )
A. 1个 B. 2个 C.3个 D. 4个

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空题:
(1)-6的倒数是_____,-6的倒数的倒数是_______,-6的相反数是______,-6的相反数的相反数是_______;
(2)当两数_____时,它们的和为0;
(3)当两数_____时,它们的积为0;
(4)当两数_____时,它们的积为1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】事件A:某人上班乘车,刚到车站车就到了;事件B:掷一枚骰子,向上一面的点数不大于6.则正确的说法是( )
A.只有事件A是随机事件
B.只有事件B是随机事件
C.都是随机事件
D.都不是随机事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下面的有理数填在相应的大括号里:(★友情提示:将各数用逗号分开)
15,﹣ ![]() ,0, ﹣30,﹣0.15,﹣128,
,0, ﹣30,﹣0.15,﹣128, ![]() , +20,﹣2.6
, +20,﹣2.6
正数集合{ ﹜;
负数集合﹛ ﹜;
整数集合﹛ ﹜;
非负数集合﹛ ﹜.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣![]() x2﹣
x2﹣![]() x+2与x轴交于A、B两点,与y轴交于点C
x+2与x轴交于A、B两点,与y轴交于点C
(1)求点A,B,C的坐标;
(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;
(3)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com