
【题目】如图,AB是⊙O的直径,点C在⊙O上,CD与⊙O相切,AD∥BC,连结OD,AC.
(1)求证:∠B=∠DCA;
(2)若 ![]() ,OD=
,OD= ![]() , 求⊙O的半径长.
, 求⊙O的半径长.
【答案】
(1)解:连接 ![]() ,
, ![]() 与
与 ![]() 相切,
相切,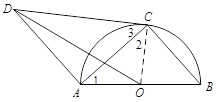
![]()
![]() 是
是 ![]() 的直径,
的直径, ![]()
![]()
![]()
![]()
![]() 即
即 ![]()
(2)解: ![]() ,
, ![]() 是
是 ![]() 的直径,
的直径, ![]()
![]()
![]()
![]()
![]()
![]()
![]() 设
设 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 在
在 ![]() 中,
中, ![]()
![]() ,解得
,解得 ![]()
![]() 的半径长为3
的半径长为3
【解析】(1)根据切线的性质可得![]() DCO=
DCO=![]() ,由直径所对的圆周角是直角可得∠ A C B =
,由直径所对的圆周角是直角可得∠ A C B = ![]() ,再结合已知条件结论可得;(2)根据已知条件可证△ABC△DCA,则DC可表示出来,在 △ O D C 中,用勾股定理可求解。
,再结合已知条件结论可得;(2)根据已知条件可证△ABC△DCA,则DC可表示出来,在 △ O D C 中,用勾股定理可求解。
【考点精析】关于本题考查的勾股定理的概念和圆周角定理,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能得出正确答案.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线的顶点为A(0,1),矩形CDEF的顶点C、F在抛物线上,点D、E在x轴上,CF交y轴于点B(0,2),且矩形其面积为8,此抛物线的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点P(x,y)在第三象限,且点P到x轴的距离为3,到y轴的距离为2,则点P的坐标是( )
A.(﹣2,﹣3)
B.(﹣2,3)
C.(2,﹣3)
D.(2,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(-1,3),B(-4,0),C(0,0)
(1)①画出将△ABC向上平移1个单位长度,再向右平移5个单位长度后得到的△A1B1C1;②画出将△ABC绕原点O顺时针方向旋转90°得到的△A2B2O;
(2)在x轴上存在一点P,满足点P到点A1与点A2的距离之和最小,请直接写出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项工程,甲、乙两公司合做,12天可以完成,共需付工费102000元;如果甲、乙两公司单独完成此项公程,乙公司所用时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1500元.
(1)甲、乙公司单独完成此项工程,各需多少天?
(2)若让一个公司单独完成这项工程,哪个公司施工费较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,排球运动员站在点O处练习发球,将球从O点正上方2 ![]() 的A处发出,把球看成点,其运行的高度
的A处发出,把球看成点,其运行的高度 ![]() 与运行的水平距离
与运行的水平距离 ![]() 满足关系式
满足关系式 ![]() .已知球网与O点的水平距离为9
.已知球网与O点的水平距离为9 ![]() ,高度为2.43
,高度为2.43 ![]() ,球场的边界距O点的水平距离为18
,球场的边界距O点的水平距离为18 ![]() .
.
(1)当 ![]() =2.6时,求
=2.6时,求 ![]() 与
与 ![]() 的关系式(不要求写出自变量
的关系式(不要求写出自变量 ![]() 的取值范围);
的取值范围);
(2)当 ![]() =2.6时,球能否越过球网?球会不会出界?请说明理由;
=2.6时,球能否越过球网?球会不会出界?请说明理由;
(3)若球一定能越过球网,又不出边界,求二次函数中 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国航空母舰“辽宁号”的满载排水量为67500吨.将数67500用科学记数法表示为( )
A.0.675×105
B.6.75×104
C.67.5×103
D.675×102
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,二次函数y=-2x2+4x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
(1)求m的值及点B的坐标;
(2)求△ABC的面积;
(3)该二次函数图象上有一点D(x,y),使S△ABD=S△ABC,请求出D点的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com