Question

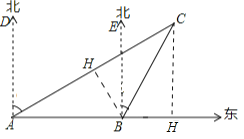
【题目】如图，一艘渔船正以30海里／时的速度由西向东追赶鱼群，在A处看见小岛C在船的北偏东60°方向上，40分钟后，渔船行至B处，此时看见小岛C在渔船的北偏东30°方向上．

（1）求A处与小岛C之间的距离；

（2）渔船到达B处后，航行方向不变，当渔船继续航行多长时间时，才能与小岛C的距离最短．

Answer 1

【答案】（1）20海里；（2）当渔船继续航行20分钟才能与小岛C的距离最短．

【解析】

（1）作BH⊥AC于H．首先证明AB=BC，AH=HC，求出HC即可解决问题；
（2）作CH⊥AB交AB的延长线于H．求出BH即可解决问题；

（1）作BH⊥AC于H．
∵∠CBD=∠CAB+∠BCA，∠CAB=30°，∠CBD=60°，
∴∠ACB=∠BAC=30°
∴BA=BC=30×=20海里．
∵BH⊥AC，
∴AH=HC=ABcos30°=10海里，

∴AC=2AH=20海里．
（2）作CH⊥AB交AB的延长线于H．
在Rt△BCH中，BH=BCcos60°=10海里，
∴时间t=小时=20分钟．
∴当渔船继续航行20分钟才能与小岛C的距离最短．