
【题目】在△ABC中,∠B=40°,过点A的直线将这个三角形分成两个等腰三角形,则∠C的度数为______________.
【答案】20°或50°或80°
【解析】
先画出图形,再根据∠B为底角或顶角两种情况讨论;由△ABD形状的改变而引起△ACD的形状发生改变,可求出∠C的度数.
解:应分四种情况进行讨论:
当AD=AC,AD=BD时,如图①所示,
∠BAD=∠B=40°,∠C=∠ADC.
∵∠BAD+∠B+∠ADB=180°,
∴∠ADB=180°-2×40°=100°,
∴∠ADC=180°-∠ADB=80°,
∴∠C=80°;
当AC=DC,BD=AD时,如图①所示,
∠DAC=∠ADC=180°-∠ADB=∠B+∠BAD=80°,
∴∠C=180°-∠ADC-∠DAC=20°;
当AD=DC,AB=AD时,如图②所示,
∠C=∠DAC,∠ADB=∠B=40°.
∴∠ADC=180°-∠ADB=140°,
∴∠C=![]() (180°-∠ADC)=20°;
(180°-∠ADC)=20°;
当AD=BD,AD=CD时,如图①所示,
∠BAD=∠B=40°,∠ADC=180°-∠ADB=∠B+∠BAD=80°,
∠C=∠DAC=![]() (180°-∠ADC)=
(180°-∠ADC)=![]() ×(180°-80°)=50°.
×(180°-80°)=50°.
综上所述,∠C的度数为80°或20°或50°.



科目:初中数学 来源: 题型:
【题目】某商场的打折活动规定:凡在本商场购物,可转动转盘一次,如图,并根据所转结果付账.

(1)分别求出打九折,打八折的概率;
(2)求不打折的概率;
(3)小红和小明分别购买了价值200元的商品,活动后一共付钱360元,求他俩获得优惠的情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
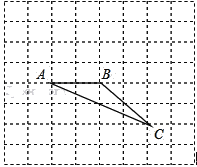
【题目】如图在8×8的正方形网格中,△ABC 的顶点在边长为1的小正方形的顶点上.
(1)填空:∠ABC= ,BC= ;
(2)若点A在网格所在的坐标平面里的坐标为(1,﹣2),请你在图中找出一点D,并作出以A、B、C、D四个点为顶点的平行四边形,求出满足条件的D点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角三角形ABC,AB=BC,直角顶点B在直线PQ上,且AD⊥PQ于D,CE⊥PQ于E.
(1)△ADB与△BEC全等吗?为什么?
(2)图1中,AD、DE、CE有怎样的等量关系?说明理由.
(3)将直线PQ绕点B旋转到如图2所示的位置,其他条件不变,那么AD、DE、CE有怎样的等量关系?直接写出结果.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘渔船正以30海里/时的速度由西向东追赶鱼群,在A处看见小岛C在船的北偏东60°方向上,40分钟后,渔船行至B处,此时看见小岛C在渔船的北偏东30°方向上.

(1)求A处与小岛C之间的距离;
(2)渔船到达B处后,航行方向不变,当渔船继续航行多长时间时,才能与小岛C的距离最短.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人玩“石头、剪刀、布”的游戏,他们在不透明的袋子中放入形状,大小均相同的15张卡片,其中写有“石头”、“剪刀”、“布”的卡片数分别为3、5、7张,两人各随机摸出一张卡片(先摸者不放回)来比胜负,并约定“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,同种卡片不分胜负.
(1)若甲先摸,则他摸出“石头”的概率是多少?
(2)若甲先摸出“石头”,则乙获胜的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(观察思考)
怎样判断两条直线是否平行?
如图①,很难看出直线a、n是否平行,可添加“第三条线”(截线c),把判断两条直线的位置关系转化为判断两个角的数量关系.我们称直线c为“辅助线”.在部分代数问题中,很难用算术直接计算出结果,于是,引入字母解决复杂问题,我们称引入的字母为“辅助元”.事实上,使用“辅助线”、“辅助元”等“辅助元素”可以更容易地解决问题.

(理解运用)
(1)计算![]() 这个算式直接计算很麻烦,请你引入合适的“辅助元”完成计算.
这个算式直接计算很麻烦,请你引入合适的“辅助元”完成计算.
(拓展提高)
(2)若关于x,y的方程组![]() 的解是
的解是![]() ,则关于x、y的方程组
,则关于x、y的方程组![]() 的解为 .
的解为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com