
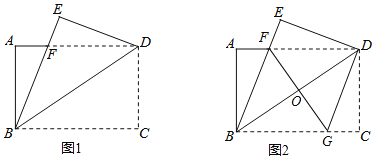
【题目】如图1,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.
(1)求证:△BDF是等腰三角形;
(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.
①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长为 .
【答案】(1)见解析;(2)①四边形BFDG是菱形.理由见解析;②FG=![]() .
.
【解析】
(1)证明△BDF是等腰三角形,可证明BF=DF,可通过证明∠EBD=∠FDB实现,利用折叠的性质和平行线的性质解决.
(2)①先判断四边形BFDG是平行四边形,再由(1)BF=FD得到结论;②要求FG的长,可先求出OF的长,在Rt△BFO中,BO可由AB、AD的长及菱形的性质求得,解决问题的关键是求出BF的长.在Rt△BFA中,知AB=6、AF+BF=AD=8,可求出BF的长,问题得以解决.
(1)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠ADB=∠CBD,
由折叠的性质可知:∠EBD=∠CBD,
∴ADB=∠EBD,
∴BF=FD
∴△BDF是等腰三角形
(2)①四边形BFDG是菱形.
理由:∵FD∥BG,DG∥BE,
∴四边形BFDG是平行四边形
又∵BF=DF,
∴四边形BFDG是菱形
②设AF=x,则FD=8-x,
∴BF=FD=8-x
在Rt△ABF中,
62+x2=(8-x)2,
解得:x=![]() ,
,
∴FD=8-![]() =
=![]() ,
,
在Rt△ABD中,∵AB=6,AD=8,
∴BD=10
∵四边形BFDG是菱形,
∴OD=![]() BD=5,FO=
BD=5,FO=![]() FG,FG⊥BD,
FG,FG⊥BD,
在Rt△ODF中,
∵FO2+DO2=FD2,即FO2+52=(![]() )2,
)2,
∴FO=![]() ,
,
∴FG=2FO=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,边长为5的正方形ABCD的对角线AC、BD相交于点P,顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O),顶点C. D都在第一象限。
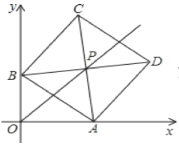
(1)当点A坐标为(4,0)时,求点D的坐标;
(2)求证:OP平分∠AOB;
(3)直接写出OP长的取值范围(不要证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义运算a![]() b=a(1-b),下面给出了关于这种运算的四个结论:
b=a(1-b),下面给出了关于这种运算的四个结论:
①2![]() (-2)=6 ②a
(-2)=6 ②a![]() b=b
b=b![]() a
a
③若a+b=0,则(a![]() a)+(b
a)+(b![]() b)=2ab ④若a
b)=2ab ④若a![]() b=0,则a=0.
b=0,则a=0.
其中正确结论的序号是 (填上你认为所有正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
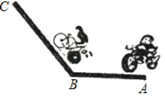
【题目】如图,现有两条乡村公路AB、BC,AB长为1200米,BC长为1600,一个人骑摩托车从A处以20m/s的速度匀速沿公路AB、BC向C处行驶;另一人骑自行车从B处以5m/s的速度从B向C行驶,并且两人同时出发.
(1)求经过多少秒摩托车追上自行车?
(2)求两人均在行驶途中时,经过多少秒两人在行进路线上相距150米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形纸片ABCD,∠A=60°,P为AB中点,折叠菱形纸片ABCD,使点C落在DP所在的直线上,得到经过点D的折痕DE,则∠DEC等于( )
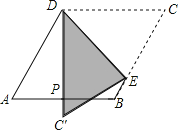
A. 60°B. 65°C. 75°D. 80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,连接EF,若BF=12,AB=10,则AE的长为( )

A. 16B. 15C. 14D. 13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AD是△ABC的中线,E为AD的中点,过点A作AF∥BC交BE延长线于点F,连接CF.
(1)如图1,求证:四边形ADCF是平行四边形;
(2)如图2,连接CE,在不添加任何辅助线的情况下,请直接写出图2中所有与△BDE面积相等的三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3…An,….将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:①抛物线的顶点M1,M2,M3,…Mn,…都在直线L:y=x上;②抛物线依次经过点A1,A2,A3…An,….则顶点M2014的坐标为_______.
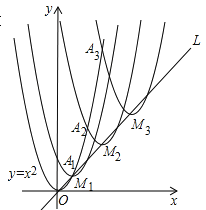
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com