
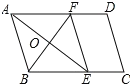
【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,连接EF,若BF=12,AB=10,则AE的长为( )

A. 16B. 15C. 14D. 13
【答案】A
【解析】
根据平行四边形的性质和角平分线的性质证明∠BAE=∠BEA,从而可得AB=BE,同理可得AB=AF,再由AF∥BE可得四边形ABEF是菱形,根据菱形的性质可得AE⊥BF,AE=2OA,OB=OF=![]() BF=6,利用勾股定理可得AO的长,进而可得AE长.
BF=6,利用勾股定理可得AO的长,进而可得AE长.
如图所示:
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB,
∵∠BAD的平分线交BC于点E,
∴∠DAE=∠BAE,
∴∠BAE=∠BEA,
∴AB=BE,同理可得AB=AF,
∴AF=BE,
∴AF//BE,AF=BE,
∴四边形ABEF是平行四边形,
∵AB=AF,
∴四边形ABEF是菱形,
∴AE⊥BF,AE=2OA,OB=OF=![]() BF=
BF=![]() =6,
=6,
∴OA=![]() =
=![]() =8,
=8,
∴AE=2OA=16,
故选A.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
【题目】教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )

A.7:20 B.7:30 C.7:45 D.7:50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简及求值:
①3ab-3b2﹣3a2+2ab﹣(5ab+2a2)+4b2 当a=-![]() ,b=-1
,b=-1
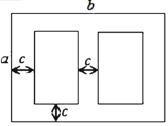
②如图是某学校草场一角,在长为b米,宽为a米的长方形场地中间,有并排两个大小一样的篮球场,两个篮球场中间以及篮球场与长方形场地边沿的距离都为c米.
(1)用代数式表示这两个篮球场的占地面积.
(2)当a=30,b=40,c=3时,计算出一个篮球场的面积.
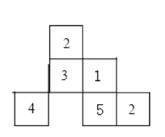
③已知由几个大小相同的小立方块搭成的几何体,从上面观察,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数.请分别画出从正面、左面看到的这个几何体的形状图.(几何体中每个小立方块的棱长都是1cm)
查看答案和解析>>
科目:初中数学 来源: 题型:
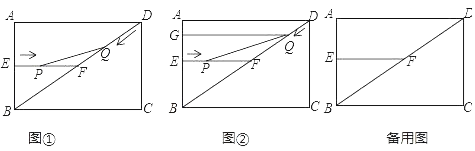
【题目】如图1,在矩形ABCD中,AB=6cm,BC=8cm,E、F分别是AB、BD的中点,连接EF,点P从点E出发,沿EF方向匀速运动,速度为1cm/s,同时,点Q从点D出发,沿DB方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(0<t<4)s,解答下列问题:
(1)求证:△BEF∽△DCB;
(2)当点Q在线段DF上运动时,若△PQF的面积为0.6cm2,求t的值;
(3)如图2过点Q作QG⊥AB,垂足为G,当t为何值时,四边形EPQG为矩形,请说明理由;
(4)当t为何值时,△PQF为等腰三角形?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
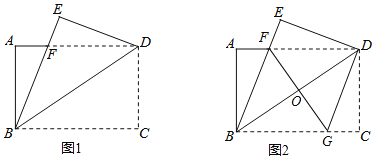
【题目】如图1,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.
(1)求证:△BDF是等腰三角形;
(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.
①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用一面长18米的墙,用篱笆围成一个矩形场地ABCD,设AD长为x米,AB长为y米,矩形的面积为S平方米.
(1)若篱笆的长为32米,求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)在(1)的条件下,求S与x的函数关系式,并求出使矩形场地的面积为120平方米的围法.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民用水实行阶梯水价,实施细则如下表:
分档水量 | 年用水量 (立方米) | 水价 (元/立方米) |
第一阶梯 | 0~180(含) | 5.00 |
第二阶梯 | 181~260(含) | 7.00 |
第三阶梯 | 260以上 | 9.00 |
例如,某户家庭年使用自来水200 m3,应缴纳:180×5+(200-180)×7=1040元;
某户家庭年使用自来水300 m3,应缴纳:180×5+(260-180)×7+(300-260)×9=1820元.
(1)小刚家2017年共使用自来水170 m3,应缴纳 元;小刚家2018年共使用自来水260 m3,应缴纳 元.
(2)小强家2018年使用自来水共缴纳1180元,他家2018年共使用了多少自来水?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一工程需在规定日期x天内完成,如果甲单独工作刚好能够按期完成:如果乙单独工作就要超过规定日期3天.
(1)甲的工作效率为 ,乙的工作效率为 .(用含x的代数式表示)
(2)若甲、乙合作2天后余下的工程由乙单独完成刚好在规定日期完成,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个有50个奇数排成的数阵,用如图所示的框去框住四个数,并求出这四个数的和,在下列给出的备选答案中,有可能是这四个数的和的是( )
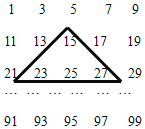
A. 114 B. 122 C. 220 D. 84
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com