
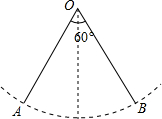
 如图,秋千链子的长度为4m,当秋千向两边摆动时,两边的摆动角度均为30°.则它摆动至最高位置与最低位置的高度之差为(4-2$\sqrt{3}$)m(结果保留根号).
如图,秋千链子的长度为4m,当秋千向两边摆动时,两边的摆动角度均为30°.则它摆动至最高位置与最低位置的高度之差为(4-2$\sqrt{3}$)m(结果保留根号). 分析 设秋千摆至最低点时的位置为C,连结AB,交OC于D.当秋千摆至最低点C时,点C为弧AB的中点,由垂径定理的推论知AB⊥OC,AD=BD,再解直角△AOD,求得OD,进而求出DC即可.
解答 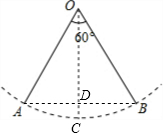 解:如图,设秋千摆至最低点时的位置为C,连结AB,交OC于D.
解:如图,设秋千摆至最低点时的位置为C,连结AB,交OC于D.
∵点C为弧AB的中点,O为圆心,
∴AB⊥OC,AD=BD,弧AC=弧BC,
∵∠AOB=60°,
∴∠AOC=30°.
∵OA=OB=OC=4,
∴AD=$\frac{1}{2}$OA=2,OD=$\sqrt{3}$AD=$\sqrt{3}$,
∴DC=OC-OD=4-2$\sqrt{3}$,
即它摆动至最高位置与最低位置的高度之差为(4-2$\sqrt{3}$)m.
故答案为(4-2$\sqrt{3}$)m.
点评 本题考查了解直角三角形的应用,垂径定理的应用,将实际问题抽象为几何问题是解题的关键.


 作业辅导系列答案
作业辅导系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x3与23 | B. | -xy2与$\frac{1}{4}$yx2 | C. | 7与-$\frac{1}{3}$ | D. | ab与7a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com