
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于A,B两点(点A在点B左侧),已知A点的横坐标是-4;
的图象交于A,B两点(点A在点B左侧),已知A点的横坐标是-4;
(1)求反比例函数的表达式;
(2)根据图象直接写出﹣![]() x﹤
x﹤![]() 的解集;
的解集;
(3)将直线l1:y=![]() x沿y向上平移后的直线l2与反比例函数y=
x沿y向上平移后的直线l2与反比例函数y=![]() 在第二象限内交于点C,如果△ABC的面积为20,求平移后的直线l2的函数表达式.
在第二象限内交于点C,如果△ABC的面积为20,求平移后的直线l2的函数表达式.
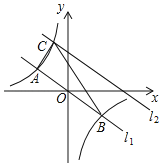
【答案】(1)![]() (2)x>4或-4<x<0 (3)y=﹣
(2)x>4或-4<x<0 (3)y=﹣![]() x+5
x+5
【解析】
(1)由正比例函数解析式确定A(-4,2),然后把A点坐标代入y=![]() 中求出k得到反比例函数解析式;
中求出k得到反比例函数解析式;
(2)通过解方程组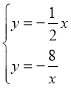 得B(4,-2),然后利用函数图象写出反比例函数图象在一次函数y=-
得B(4,-2),然后利用函数图象写出反比例函数图象在一次函数y=-![]() x上方所对应的自变量的范围,从而得到-
x上方所对应的自变量的范围,从而得到-![]() x<
x<![]() 的解集;
的解集;
(3)设直线l2交x轴于D,连接AD、BD,如图,利用三角形面积公式得S△ADB=S△ACB=20,则![]() ×OD×2+
×OD×2+![]() ×OD×2=30,求出OD得到D(10,0),利用两直线平行可设直线l2的解析式为y=-
×OD×2=30,求出OD得到D(10,0),利用两直线平行可设直线l2的解析式为y=-![]() x+b,然后把D点坐标代入求出b得到直线l2的解析式为y=-
x+b,然后把D点坐标代入求出b得到直线l2的解析式为y=-![]() x+5.
x+5.
解:(1)∵直线l1:y=﹣![]() x经过点A,A点的横坐标是-4
x经过点A,A点的横坐标是-4
∴当x=﹣4时,y=2,
∴A(﹣4,2),
∵反比例函数y=![]() 的图象经过点A,
的图象经过点A,
∴k=﹣4×2=﹣8,
∴反比例函数的表达式为y=﹣![]() ;
;
(2)解方程组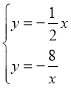 得
得![]() 或
或![]() ,
,
∴B(4,﹣2),
∴不等式﹣![]() x﹤
x﹤![]() 的解集为xspan>>4或-4<x<0;
的解集为xspan>>4或-4<x<0;
(3)如图,设平移后的直线l2与x轴交于点D,连接AD,BD,
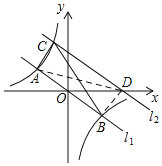
∵CD∥AB,
∴△ABC的面积与△ABD的面积相等,
∵△ABC的面积为20,
∴S△AOD+S△BOD=20,即![]() OD(|yA|+|yB|)=20,
OD(|yA|+|yB|)=20,
∴![]() ×OD×4=20,
×OD×4=20,
∴OD=10,
∴D(10,0),
设平移后的直线l2的函数表达式为y=﹣![]() x+b,
x+b,
把D(10,0)代入,可得0=﹣![]() ×10+b,
×10+b,
解得b=5,
∴平移后的直线l2的函数表达式为y=﹣![]() x+5.
x+5.


科目:初中数学 来源: 题型:
【题目】实行垃圾资源化利用,是社会文明水平的一个重要体现.某环保公司研发的甲、乙两种智能设备可利用最新技术将干垃圾变身为燃料棒.某垃圾处理厂从环保公司购入以上两种智能设备,若干已知购买甲型智能设备花费360万元,购买乙型智能设备花费480万元,购买的两种设备数量相同,且两种智能设备的单价和为140万元.
(1)求甲乙两种智能设备单价;
(2)垃圾处理厂利用智能设备生产燃料棒,并将产品出售.已知燃料棒的成本由人力成本和物资成本两部分组成,其中物资成本占总成本的40%,且生产每吨燃料棒所需人力成本比物资成本的![]() 倍还多10元,调查发现:若燃料棒售价为每吨200元,平均每天可售出350吨,而当销售价每降低1元,平均每天可多售出5吨,但售价在每吨200元基础上降价幅度不超过7%,
倍还多10元,调查发现:若燃料棒售价为每吨200元,平均每天可售出350吨,而当销售价每降低1元,平均每天可多售出5吨,但售价在每吨200元基础上降价幅度不超过7%,
①垃圾处理厂想使这种燃料棒的销售利润平均每天达到36080元,求每吨燃料棒售价应为多少元?
②每吨燃料棒售价应为多少元时,这种燃料棒平均每天的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校想知道九年级学生对我国倡导的“一带一路”的了解程度,随机抽取部分九年级学生进行问卷调查,问卷设有4个选项(每位被调查的学生必选且只选一项):A.非常了解.B.了解.C.知道一点.D.完全不知道.将调查的结果绘制如下两幅不完整的统计图,请根据两幅统计图中的信息,解答下列问题:
(1)求本次共调查了多少学生?
(2)补全条形统计图;
(3)该校九年级共有600名学生,请你估计“了解”的学生约有多少名?
(4)在“非常了解”的3人中,有2名女生,1名男生,老师想从这3人中任选两人做宣传员,请用列表或画树状图法求出被选中的两人恰好是一男生一女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校全体学生积极参加校团委组织的“献爱心捐款”活动,为了解捐款情况,随机抽取了部分学生并对他们的捐款情况作了统计,绘制了两幅不完整的统计图(统计图中每组含最小值,不含最大值).请依据图中信息解答下列问题:

(1)求随机抽取的学生人数;
(2)填空:(直接填答案)
①“20元~25元”部分对应的圆心角度数为______;
②捐款的中位数落在______(填金额范围);
(3)若该校共有学生3500人,请估算全校捐款不少于20元的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
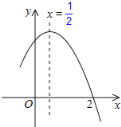
【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴x=![]() ,且经过点(2,0),下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(﹣
,且经过点(2,0),下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(﹣![]() ,y1),(
,y1),(![]() ,y2)是抛物线上的两点,则y1>y2,其中说法正确的序号是_____
,y2)是抛物线上的两点,则y1>y2,其中说法正确的序号是_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人民生活水平的提高和环境的不断改善,带动了旅游业的发展.某市旅游景区有A,B,C,D四个著名景点,该市旅游部门统计绘制出2019年游客去各景点情况统计图,根据给出的信息解答下列问题:
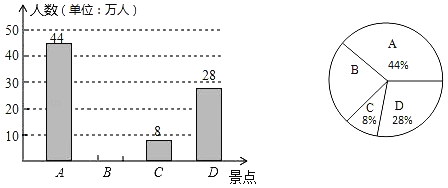
(1)2019年该市旅游景区共接待游客 万人,扇形统计图中C景点所对应的圆心角的度数是 度;
(2)把条形统计图补充完整;
(3)甲,乙两位同学去该景区旅游,用树状图或列表法,求甲,乙两位同学在A,B,D三个景点中,同时选择去同一景点的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
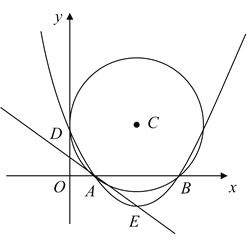
【题目】我们把方程(x- m)2+(y-n)2=r2称为圆心为(m,n)、半径长为r的圆的标准方程.例如,圆心为(1,-2)、半径长为3的圆的标准方程是(x- 1)2+(y+2)2=9.在平面直角坐标系中,圆C与轴交于点A.B.且点B的坐标为(8.0),与y轴相切于点D(0, 4),过点A,B,D的抛物线的顶点为E.
(1)求圆C的标准方程;
(2)试判断直线AE与圆C的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
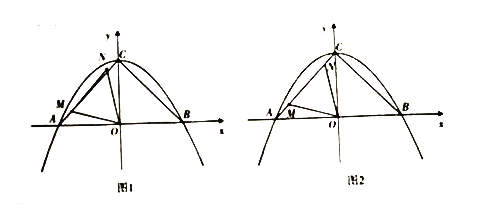
【题目】如图1,抛物线![]() 与x轴,y轴的正半轴分别交于点
与x轴,y轴的正半轴分别交于点![]() 和点
和点![]() ,与x轴负半轴交于点A,动点M从点A出发沿折线
,与x轴负半轴交于点A,动点M从点A出发沿折线![]() 向终点B匀速运动,将线段
向终点B匀速运动,将线段![]() 绕点O顺时针旋转
绕点O顺时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() .
.
(1)求抛物线![]() 的函数表达式;
的函数表达式;
(2)如图2,当点N在线段![]() 上时,求证:
上时,求证:![]() ;
;
(3)当点N在线段![]() 上时,直接写出此时直线
上时,直接写出此时直线![]() 与抛物线交点的纵坐标;
与抛物线交点的纵坐标;
(4)设![]() 的长度为n,直接写出在点M移动的过程中,
的长度为n,直接写出在点M移动的过程中,![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com