
【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴x=![]() ,且经过点(2,0),下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(﹣
,且经过点(2,0),下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(﹣![]() ,y1),(
,y1),(![]() ,y2)是抛物线上的两点,则y1>y2,其中说法正确的序号是_____
,y2)是抛物线上的两点,则y1>y2,其中说法正确的序号是_____
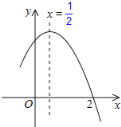
【答案】①②
【解析】
①根据抛物线开口方向、对称轴位置、抛物线与y轴交点位置求得a、b、c的符号;
②根据对称轴求出b=-a;
③把x=2代入函数关系式,结合图象判断函数值与0的大小关系;
④求出点(-![]() ,y1)关于对称轴x=
,y1)关于对称轴x=![]() 的对称点的坐标,根据二次函数的增减性即可判断y1和y2的大小.
的对称点的坐标,根据二次函数的增减性即可判断y1和y2的大小.
如图,
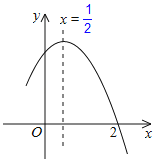
①∵二次函数的图象开口向下,
∴a<0,
∵二次函数的图象交y轴的正半轴于一点,
∴c>0,
∵对称轴是直线x=-![]() =
=![]() ,
,
∴b=-a>0,
∴abc<0.
故①正确;
②∵由①中知b=-a,
∴a+b=0,
故②正确;
③把x=2代入y=ax2+bx+c得:y=4a+2b+c,
∵抛物线经过点(2,0),
∴当x=2时,y=0,即4a+2b+c=0.
故③错误;
④∵(-![]() ,y1)关于对称轴x=
,y1)关于对称轴x=![]() 的对称点的坐标是(
的对称点的坐标是(![]() ,y1),
,y1),
又∵当x>![]() 时,y随x的增大而减小,
时,y随x的增大而减小,![]() <
<![]() ,
,
∴y1<y2.
故④错误;
综上所述,正确的结论是①②.
故答案为:①②.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
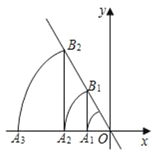
【题目】如图,直线l:y=﹣![]() x,点A1的坐标为(﹣1,0),过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴正半轴于点A2;再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴正半轴于点A3;…,按此作法进行下去点A2020的坐标为_____.
x,点A1的坐标为(﹣1,0),过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴正半轴于点A2;再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴正半轴于点A3;…,按此作法进行下去点A2020的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
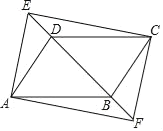
【题目】如图,在ABCD中,点E,F是直线BD上的两点,DE=BF.
(1)求证:四边形AFCE是平行四边形.
(2)若BD⊥AD,AB=5,AD=3,四边形AFCE是矩形,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
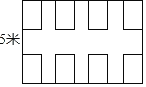
【题目】如图所示的是一个宽5米的餐厅,只能放8张餐桌.现计划扩建增加座位,只能对原宽度进行加长,设加长后的长度为m米.若餐厅的餐桌数为y,经计算,得到如下数据:(注:m和y都为正整数)
m(米) | 5 | 8 | 11 | 14 | …… |
餐桌数y(张) | 8 | 12 | 16 | …… |
(1)根据表中数据的规律,完成以上表格;
(2)求出y关于m的函数解析式;
(3)若这家餐厅至少要有80张餐桌,求m的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
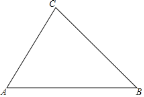
【题目】如图,已知△ABC,请用直尺(不带刻度),和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹).
(1)作菱形AMNP,使点M,N、P在边AB、BC、CA上;
(2)当∠A=60°,AB=4,AC=3时,求菱形AMNP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
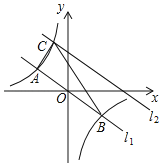
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于A,B两点(点A在点B左侧),已知A点的横坐标是-4;
的图象交于A,B两点(点A在点B左侧),已知A点的横坐标是-4;
(1)求反比例函数的表达式;
(2)根据图象直接写出﹣![]() x﹤
x﹤![]() 的解集;
的解集;
(3)将直线l1:y=![]() x沿y向上平移后的直线l2与反比例函数y=
x沿y向上平移后的直线l2与反比例函数y=![]() 在第二象限内交于点C,如果△ABC的面积为20,求平移后的直线l2的函数表达式.
在第二象限内交于点C,如果△ABC的面积为20,求平移后的直线l2的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司用6000元购进A,B两种电话机25台,购买A种电话机与购买B种电话机的费用相等.已知A种电话机的单价是B种电话机单价的1.5倍.
(1)求A,B两种电话机的单价各是多少?
(2)若计划用不超过8000元的资金再次购进A,B两种话机共30台,已知A,B两种电话机的进价不变,求最多能购进多少台A种电话机?
查看答案和解析>>
科目:初中数学 来源: 题型:
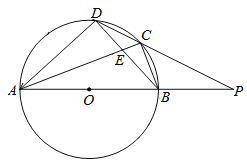
【题目】如图,在四边形ABCD中,以AB为直径的半圆O经过点C,D.AC与BD相交于点E,CD2=CE·CA,分别延长AB,DC相交于点P,PB=BO,CD=2![]() .则BO的长是_________.
.则BO的长是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com