
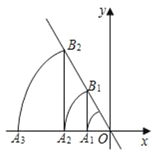
【题目】如图,直线l:y=﹣![]() x,点A1的坐标为(﹣1,0),过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴正半轴于点A2;再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴正半轴于点A3;…,按此作法进行下去点A2020的坐标为_____.
x,点A1的坐标为(﹣1,0),过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴正半轴于点A2;再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴正半轴于点A3;…,按此作法进行下去点A2020的坐标为_____.
科目:初中数学 来源: 题型:
【题目】国家教育部提出“每天锻炼一小时,健康工作五十年,幸福生活一辈子”.万州区某中学对九年级部分学生进行问卷调查“你最喜欢的锻炼项目是什么?”,规定从“打球”,“跑步”,“游泳”,“跳绳”,“其他”五个选项中选择自己最喜欢的项目,且只能选择一个项目,并将调查结果绘制成如下两幅不完整的统计图.
最喜欢的锻炼项目 | 人数 |
打球 | 120 |
跑步 |
|
游泳 |
|
跳绳 | 30 |
其他 |
|
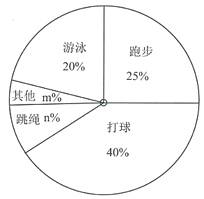
(1)这次问卷调查的学生总人数为 ,人数![]() ;
;
(2)扇形统计图中,![]() ,“其他”对应的扇形的圆心角的度数为 度;
,“其他”对应的扇形的圆心角的度数为 度;
(3)若该年级有1200名学生,估计喜欢“跳绳”项目的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国古代算书《算法统宗》中有这样一道题:甲赶群羊逐草茂,乙拽肥羊随其后,戏问甲及一百否?甲云所说无差谬,若得这般一群凑,再添半群小半(注:四分之一的意思)群,得你一只来方凑,玄机奥妙谁参透?大意是说:牧羊人赶着一群羊去寻找草长得茂盛的地方放牧,有一个过路人牵着1只肥羊从后面跟了上来,他对牧羊人说你赶的这群羊大概有100只吧?牧羊人答道:如果这一群羊加上1倍,再加上原来羊群的一半,又加上原来这群羊的四分之一,连你牵着的这只肥羊也算进去,才刚好满100只你知道牧羊人放牧的这群羊一共有多少只吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 与x轴交于A、B两点,与y轴交于C点,连接
与x轴交于A、B两点,与y轴交于C点,连接![]() 、
、![]() ,已知点A、C的坐标为
,已知点A、C的坐标为![]() 、
、![]() .
.
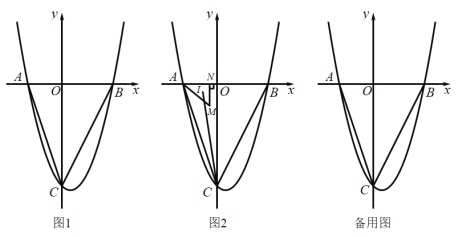
(1)求抛物线的表达式;
(2)点P是线段![]() 下方抛物线上的一动点,如果在x轴上存在点Q,使得以点B、C、P、Q为顶点的四边形为平行四边形,求点Q的坐标;
下方抛物线上的一动点,如果在x轴上存在点Q,使得以点B、C、P、Q为顶点的四边形为平行四边形,求点Q的坐标;
(3)如图2,若点M是![]() 内一动点,且满足
内一动点,且满足![]() ,过点M作
,过点M作![]() ,垂足为N,设
,垂足为N,设![]() 的内心为I,试求
的内心为I,试求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某个体地摊经销一批小商品,每件商品的成本为8元.据市场分析,销售单价定为10元时,每天能售出200件;现采用提高商品售价,减少销售量的办法增加利润,若销售单价每涨1元,每天的销售量就减少20件,设销售单价为每件x元,销售量为y件.
(1)写出y与x函数关系式.
(2)若想每天的销售利润恰为640元,同时又要使顾客得到实惠,这种小商品每件售价应定为多少元?
(3)这种小商品每件售价应定为多少元时,每天的销售利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实行垃圾资源化利用,是社会文明水平的一个重要体现.某环保公司研发的甲、乙两种智能设备可利用最新技术将干垃圾变身为燃料棒.某垃圾处理厂从环保公司购入以上两种智能设备,若干已知购买甲型智能设备花费360万元,购买乙型智能设备花费480万元,购买的两种设备数量相同,且两种智能设备的单价和为140万元.
(1)求甲乙两种智能设备单价;
(2)垃圾处理厂利用智能设备生产燃料棒,并将产品出售.已知燃料棒的成本由人力成本和物资成本两部分组成,其中物资成本占总成本的40%,且生产每吨燃料棒所需人力成本比物资成本的![]() 倍还多10元,调查发现:若燃料棒售价为每吨200元,平均每天可售出350吨,而当销售价每降低1元,平均每天可多售出5吨,但售价在每吨200元基础上降价幅度不超过7%,
倍还多10元,调查发现:若燃料棒售价为每吨200元,平均每天可售出350吨,而当销售价每降低1元,平均每天可多售出5吨,但售价在每吨200元基础上降价幅度不超过7%,
①垃圾处理厂想使这种燃料棒的销售利润平均每天达到36080元,求每吨燃料棒售价应为多少元?
②每吨燃料棒售价应为多少元时,这种燃料棒平均每天的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明与推断:
①求证:四边形CEGF是正方形;
②推断:![]() 的值为 :
的值为 :
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:
(3)拓展与运用:
正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2![]() ,则BC= .
,则BC= .

查看答案和解析>>
科目:初中数学 来源: 题型:
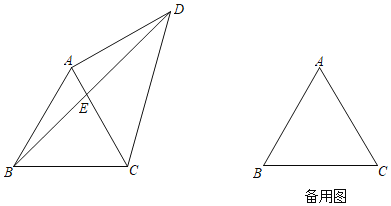
【题目】如图,△ABC是边长为2的等边三角形,点D与点B分别位于直线AC的两侧,且AD=AC,连结BD、CD,BD交直线AC于点E.
(1)当∠CAD=90°时,求线段AE的长.
(2)过点A作AH⊥CD,垂足为点H,直线AH交BD于点F,
①当∠CAD<120°时,设AE=x,y=![]() (其中S△BCE表示△BCE的面积,S△AEF表示△AEF的面积),求y关于x的函数关系式,并写出x的取值范围;
(其中S△BCE表示△BCE的面积,S△AEF表示△AEF的面积),求y关于x的函数关系式,并写出x的取值范围;
②当![]() 时,请直接写出线段AE的长.
时,请直接写出线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
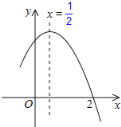
【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴x=![]() ,且经过点(2,0),下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(﹣
,且经过点(2,0),下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(﹣![]() ,y1),(
,y1),(![]() ,y2)是抛物线上的两点,则y1>y2,其中说法正确的序号是_____
,y2)是抛物线上的两点,则y1>y2,其中说法正确的序号是_____
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com