
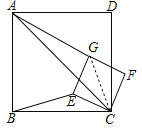
【题目】如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明与推断:
①求证:四边形CEGF是正方形;
②推断:![]() 的值为 :
的值为 :
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:
(3)拓展与运用:
正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2![]() ,则BC= .
,则BC= .

【答案】(1)①四边形CEGF是正方形;②![]() ;(2)线段AG与BE之间的数量关系为AG=
;(2)线段AG与BE之间的数量关系为AG=![]() BE;(3)3
BE;(3)3![]()
【解析】(1)①由![]() 、
、![]() 结合
结合![]() 可得四边形CEGF是矩形,再由
可得四边形CEGF是矩形,再由![]() 即可得证;
即可得证;
②由正方形性质知![]() 、
、![]() ,据此可得
,据此可得![]() 、
、![]() ,利用平行线分线段成比例定理可得;
,利用平行线分线段成比例定理可得;
(2)连接CG,只需证![]() ∽
∽![]() 即可得;
即可得;
(3)证![]() ∽
∽![]() 得
得![]() ,设
,设![]() ,知
,知![]() ,由
,由![]() 得
得![]() 、
、![]() 、
、![]() ,由
,由![]() 可得a的值.
可得a的值.
(1)①∵四边形ABCD是正方形,
∴∠BCD=90°,∠BCA=45°,
∵GE⊥BC、GF⊥CD,
∴∠CEG=∠CFG=∠ECF=90°,
∴四边形CEGF是矩形,∠CGE=∠ECG=45°,
∴EG=EC,
∴四边形CEGF是正方形;
②由①知四边形CEGF是正方形,
∴∠CEG=∠B=90°,∠ECG=45°,
∴![]() ,GE∥AB,
,GE∥AB,
∴![]() ,
,
故答案为:![]() ;
;
(2)连接CG,
由旋转性质知∠BCE=∠ACG=α,
在Rt△CEG和Rt△CBA中,
![]() =cos45°=
=cos45°=![]() 、
、![]() =cos45°=
=cos45°=![]() ,
,
∴![]() =
=![]() ,
,
∴△ACG∽△BCE,
∴![]() ,
,
∴线段AG与BE之间的数量关系为AG=![]() BE;
BE;
(3)∵∠CEF=45°,点B、E、F三点共线,
∴∠BEC=135°,
∵△ACG∽△BCE,
∴∠AGC=∠BEC=135°,
∴∠AGH=∠CAH=45°,
∵∠CHA=∠AHG,
∴△AHG∽△CHA,
∴![]() ,
,
设BC=CD=AD=a,则AC=![]() a,
a,
则由![]() 得
得![]() ,
,
∴AH=![]() a,
a,
则DH=AD﹣AH=![]() a,CH=
a,CH=![]() =
=![]() a,
a,
∴由![]() 得
得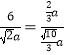 ,
,
解得:a=3![]() ,即BC=3
,即BC=3![]() ,
,
故答案为:3![]() .
.


 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】已知整数a0,a1,a2,a3,a4,…,满足下列条件:a0=0,a1=﹣|a0+1|,a2=﹣|a1+2|,a3=﹣|a2+3|,…,以此类推,a2019的值是( )
A. ﹣1009B. ﹣1010C. ﹣2018D. ﹣2020
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某摩托车厂本周计划每日生产450辆摩托车,由于工人实行轮休, 每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表: [增加的辆数为正数,减少的辆数为负数]
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
(1)本周星期六生产多少辆摩托车?
(2)本周总产量与计划产量相比,是增加了还是减少了?为什么?
(3)产量最多的那天比产量最少的那天多生产多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
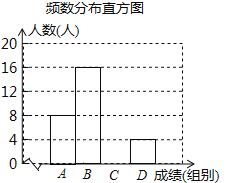
【题目】“品中华诗词,寻文化基因”.某校举办了第二届“中华诗词大赛”,将该校八年级参加竞赛的学生成绩统计后,绘制了如下不完整的频数分布统计表与频数分布直方图.
频数分布统计表
组别 | 成绩x(分) | 人数 | 百分比 |
A | 60≤x<70 | 8 | 20% |
B | 70≤x<80 | 16 | m% |
C | 80≤x<90 | a | 30% |
D | 90≤<x≤100 | 4 | 10% |
请观察图表,解答下列问题:
(1)表中a= ,m= ;
(2)补全频数分布直方图;
(3)D组的4名学生中,有1名男生和3名女生.现从中随机抽取2名学生参加市级竞赛,则抽取的2名学生恰好是一名男生和一名女生的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,DE垂直平分AB.

(1)若AB=AC=10cm,BC=6cm,求△BCE的周长;
(2)若∠A=40°,求∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,下面四个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④AP垂直平分RS.其中正确结论的序号是 (请将所有正确结论的序号都填上).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抚顺某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了多少名学生?
(2)求测试结果为C等级的学生数,并补全条形图;
(3)若该中学八年级共有700名学生,请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名?
(4)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交x轴于A,B两点(点A在点B的右侧),交y轴于点
交x轴于A,B两点(点A在点B的右侧),交y轴于点
C,顶点为D,对称轴分别交x轴、AC于点E、F,点P是射线DE上一动点,过点P作AC的平行线
MN交x轴于点H,交抛物线于点M,N(点M位于对称轴的左侧).设点P的纵坐标为t..
(1)求抛物线的对称轴及点A的坐标.
(2)当点P位于EF的中点时,求点M的坐标.
(3)① 点P在线段DE上运动时,当![]() 时,求t的值.
时,求t的值.
② 点Q是抛物线上一点,点P在整个运动过程中,满足以点C,P,M,Q为顶点的四边形是平行
四边形时,则此时t的值是 (请直接写出答案).

查看答案和解析>>
科目:初中数学 来源: 题型:
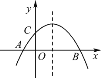
【题目】如图,已知抛物线![]() (m>0)与x轴相交于点A,B,与y轴相交于点C,且点A在点B的左侧.
(m>0)与x轴相交于点A,B,与y轴相交于点C,且点A在点B的左侧.
(1)若抛物线过点(2,2),求抛物线的解析式;
(2)在(1)的条件下,抛物线的对称轴上是否存在一点H,使AH+CH的值最小,若存在,求出点H的坐标;若不存在,请说明理由;
(3)在第四象限内,抛物线上是否存在点M,使得以点A,B,M为顶点的三角形与△ACB相似?若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com