
【题目】如图,抛物线![]() 交x轴于A,B两点(点A在点B的右侧),交y轴于点
交x轴于A,B两点(点A在点B的右侧),交y轴于点
C,顶点为D,对称轴分别交x轴、AC于点E、F,点P是射线DE上一动点,过点P作AC的平行线
MN交x轴于点H,交抛物线于点M,N(点M位于对称轴的左侧).设点P的纵坐标为t..
(1)求抛物线的对称轴及点A的坐标.
(2)当点P位于EF的中点时,求点M的坐标.
(3)① 点P在线段DE上运动时,当![]() 时,求t的值.
时,求t的值.
② 点Q是抛物线上一点,点P在整个运动过程中,满足以点C,P,M,Q为顶点的四边形是平行
四边形时,则此时t的值是 (请直接写出答案).

【答案】(1) (6,0);(2) M ![]() ;(3) ①
;(3) ①![]() ;
;
② ![]() 或
或![]() .
.
【解析】(1)根据对称轴公式即可直接求得对称轴方程,当y=0时,![]() ,解方程即可求出点A的坐标.
,解方程即可求出点A的坐标.
(2)求出点![]() 的坐标,求得直线方程
的坐标,求得直线方程![]() 联立方程即可求得点
联立方程即可求得点![]() 的坐标.
的坐标.
(3)①过点M作MK⊥x轴交于点K. 由MK//EF,![]() ,得
,得![]() MK=HK=3t,OK=3t-(2+t)=2t-2. 即M(2-2t,3t),列方程求解即可.
MK=HK=3t,OK=3t-(2+t)=2t-2. 即M(2-2t,3t),列方程求解即可.
②根据平行四边形的性质进行计算即可.
(1)对称轴直线x=![]() =2.
=2.
当y=0时,![]()
解得![]() .
.
所以对称轴为直线x=2,点A的坐标为(6,0).
(2)如图1,∵A(6,0),C(0,6)

∴OA=OC且∠AOC=90°
∵EF//y轴∴△AEF为等腰直角三角形
∴AE=EF=4若点P位于EF的中点,且MP//AC
则点H为AE的中点.
∴P(2,2),H(4,0)
∴![]()
则![]()
解得:![]() (舍去)
(舍去)
∴![]()
∴M ![]() .
.
(3)①如图2, 过点M作MK⊥x轴交于点K.
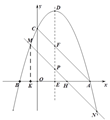
∵点P在线段DE上运动,则t > 0.
P(2,t),PE=EH=t.
由MK//EF,![]()
得:![]()
∴MK=HK=3t,OK=3t-(2+t)=2t-2.
即M(2-2t,3t)
![]() ,
,
化简:![]()
解得: ![]() (舍去)
(舍去)
∴点P在线段DE上运动时,当![]() 时, t的值为
时, t的值为![]()
② ![]() 或
或![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,下列结论:①∠AED=90°②∠ADE=∠CDE③DE=BE④AD=AB+CD,四个结论中成立的是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明与推断:
①求证:四边形CEGF是正方形;
②推断:![]() 的值为 :
的值为 :
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:
(3)拓展与运用:
正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2![]() ,则BC= .
,则BC= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(-10,0),B(-6,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB,∠CDA=90°.点P从点Q(8,0)出发,沿x轴向左以每秒1个单位长的速度向点A匀速运动,运动时间为t秒.
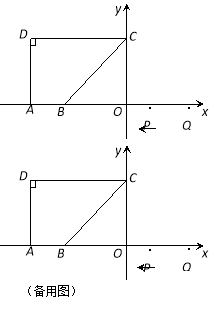
(1)求点C的坐标.
(2)当∠BCP=15°时,求t的值.
(3)以PC为直径作圆,当该圆与四边形ABCD的边(或边所在的直线)相切时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从百货大楼出发送货,向东走了4千米到达小明家,继续向东走了1.5千米到达小红家,然后向西走了8.5千米到达小刚家,最后返回百货大楼.
![]()
(1)以百货大楼为原点,向东为正方向,1个单位长度表示1千米,请在数轴上标出小明、小红、小刚家的位置.(小明家用点![]() 表示,小红家用点
表示,小红家用点![]() 表示,小刚家用点
表示,小刚家用点![]() 表示)
表示)
(2)求这辆货车此次送货(从出发到返回百货大楼)总共走的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC中,AB=![]() ,AH⊥BC于点H,过点B作BD⊥AB交线段AH的延
,AH⊥BC于点H,过点B作BD⊥AB交线段AH的延
长线于点D,连结CD. 点E为线段AD上一点(不与点A,D重合),过点E作EF∥AB交BC于点
F,以EF为直径作⊙O. 设AE的长为![]() .
.
(1)求线段CD的长度.
(2)当点E在线段AH上时,用含x的代数式表示EF的长度.
(3) 当⊙O与四边形ABDC的一边所在直线相切时,求所有满足条件的![]() 的值.
的值.
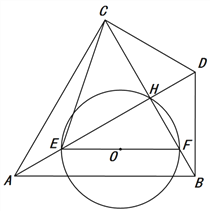
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,且
,且![]() 满足
满足![]() ,
,![]() 为原点.若动点
为原点.若动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿数轴向右匀速运动,设运动的时间为
个单位长度的速度沿数轴向右匀速运动,设运动的时间为![]() (秒) .
(秒) .
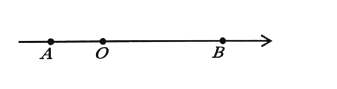
![]() 求
求![]() 的值;
的值;
![]() 当点
当点![]() 运动到线段
运动到线段![]() 上时,分别取
上时,分别取![]() 和
和![]() 的中点
的中点![]() ,试探究下列结论:
,试探究下列结论:
①![]() 的值为定值;②
的值为定值;②![]() 的值为定值,
的值为定值,
其中有且只有一个是正确的,请将正确的选出来并求出该值;
![]() 当点
当点![]() 从点
从点![]() 出发运动到点
出发运动到点![]() 时,另一动点
时,另一动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度在
个单位长度的速度在![]() 间往返运动,当
间往返运动,当![]() 时,求动点
时,求动点![]() 运动的时间
运动的时间![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某剧院的观众席的座位为扇形,且按下列分式设置:
排数(x) | 1 | 2 | 3 | 4 | … |
座位数(y) | 50 | 53 | 56 | 59 | … |
(1)按照上表所示的规律,当x每增加1时,y如何变化?
(2)写出座位数y与排数x之间的关系式;
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推广阳光体育“大课间”活动,我市某中学决定在学生中开设A:实心球.B:立定跳远,C:跳绳,D:跑步四种活动项目.为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图.请结合图中的信息解答下列问题:
(1)在这项调查中,共调查了多少名学生?
(2)请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比,并将两个统计图补充完整;
(3)若调查到喜欢“跳绳”的5名学生中有3名男生,2名女生.现从这5名学生中任意抽取2名学生.请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com