
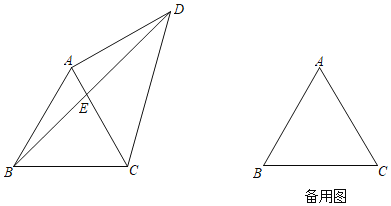
����Ŀ����ͼ����ABC�DZ߳�Ϊ2�ĵȱ������Σ���D���B�ֱ�λ��ֱ��AC�����࣬��AD��AC������BD��CD��BD��ֱ��AC�ڵ�E��
��1������CAD��90��ʱ�����߶�AE�ij���
��2������A��AH��CD������Ϊ��H��ֱ��AH��BD�ڵ�F��
������CAD��120��ʱ����AE��x��y��![]() ������S��BCE��ʾ��BCE�������S��AEF��ʾ��AEF�����������y����x�ĺ�����ϵʽ����д��x��ȡֵ��Χ��
������S��BCE��ʾ��BCE�������S��AEF��ʾ��AEF�����������y����x�ĺ�����ϵʽ����д��x��ȡֵ��Χ��
����![]() ʱ����ֱ��д���߶�AE�ij���
ʱ����ֱ��д���߶�AE�ij���
���𰸡���1��4��2![]() ����2����y��
����2����y��![]() ��0��x��2������AE�ij�Ϊ1��
��0��x��2������AE�ij�Ϊ1��![]() ��
��
��������
��1����֤����EBC��45��������E��EG��BC������Ϊ��G��AE��x����EC��2��x������BG��EG�����������x���ɵó��𰸣�
��2����֤����AEF�ס�BEC���ɵ�![]() ���ɴ˹�����ϵʽ���ɽ�����⣮
���ɴ˹�����ϵʽ���ɽ�����⣮
�ڷ��������Σ�����CAD��120��ʱ����120������CAD��180��ʱ���ֱ�ó�������⼴��
�⣺��1���ߡ�ABC�ǵȱ������Σ�
��AB��BC��AC��2����BAC����ABC����ACB��60����
��AD��AC��
��AD��AB��
���ABD����ADB��
�ߡ�ABD+��ADB+��BAC+��CAD��180������CAD��90������ABD��15����
���EBC��45����
����E��EG��BC��������G��
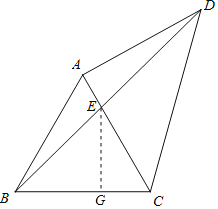
��AE��x����EC��2��x��
��Rt��CGE����ACB��60����
��EG��ECsin��ACB��![]() ��2��x����CG��ECcos��ACB��1��
��2��x����CG��ECcos��ACB��1��![]() x��
x��
��BG��2��CG��1+![]() x��
x��
��Rt��BGE����EBC��45����
��1+![]() ��2��x����
��2��x����
���x��4��2![]() ��
��
���߶�AE�ij���4��2![]() ��
��
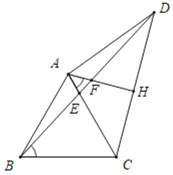
��2���ٵ���CAD��120��ʱ��
���ABD���������BDA��������DAC����BAD����BAC��120����2����
��AD��AC��AH��CD��
���CAF��![]() ��DAC��60��������
��DAC��60��������
�֡ߡ�AEF��60��+����
���AFE��60����
���AFE����ACB��
�֡ߡ�AEF����BEC��
���AEF�ס�BEC��
��![]() ��
��
�ɣ�1������Rt��CGE�У�BG��1+![]() x��EG��
x��EG��![]() ��2��x����
��2��x����
��BE2��BG2+EG2��x2��2x+4��
��y��![]() ��0��x��2����
��0��x��2����
����ͼ
y��![]() ������
������![]() ��
��
������3x2+x��2��0��
���x��![]() ��1����ȥ����
��1����ȥ����
��AE��![]() ��
��
��120������CAD��180��ʱ��ͬ���ɵ�y��![]() ��
��
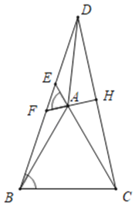
��y��![]() ʱ��
ʱ��![]() ��
��
������3x2��x��2��0��
���x����![]() ����ȥ����1��
����ȥ����1��
��AE��1��
�ۺ����Ͽɵ�AE�ij�Ϊ1��![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ��
��![]() ���������
���������![]() ��
��![]() ��ֱ��
��ֱ��![]() ������
������![]() ��ֱ��
��ֱ��![]() ��������
��������![]() ��һ������ĺ�������4�����ǵ�ͼ����ͼ��ʾ�������½��ۣ�
��һ������ĺ�������4�����ǵ�ͼ����ͼ��ʾ�������½��ۣ�
�ْ����߶Գ�����![]() ��
��
��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
����![]() ����
����![]() ��
��
������ȷ�ĸ���Ϊ�� ��
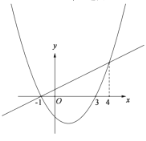
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
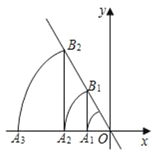
����Ŀ����ͼ��ֱ��l��y����![]() x����A1������Ϊ����1��0��������A1��x��Ĵ��߽�ֱ��l�ڵ�B1����ԭ��OΪԲ�ģ�OB1��Ϊ�뾶������x���������ڵ�A2���ٹ���A2��x��Ĵ��߽�ֱ��l�ڵ�B2����ԭ��OΪԲ�ģ�OB2��Ϊ�뾶������x���������ڵ�A3��������������������ȥ��A2020������Ϊ_____��
x����A1������Ϊ����1��0��������A1��x��Ĵ��߽�ֱ��l�ڵ�B1����ԭ��OΪԲ�ģ�OB1��Ϊ�뾶������x���������ڵ�A2���ٹ���A2��x��Ĵ��߽�ֱ��l�ڵ�B2����ԭ��OΪԲ�ģ�OB2��Ϊ�뾶������x���������ڵ�A3��������������������ȥ��A2020������Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ȫ���������Ϊ���������һ������֪ʶ������С�������ö��������ԣ�Ҫ��ְ�ȥ����Ʊ�����ְ�ֻ���һ����Ʊ����ô˭ȥ�ͳ������⣬С���뵽һ���취��ͨ������Ϸ����˭ȥ����Ϸ�����ǣ��ڲ����Ŀڴ��зֱ����2����ɫ��1����ɫ��ƹ�������dz���ɫ�������ͬ����Ϸʱ�������ôӿڴ�����������1��ƹ���������ɫ��Żز�ҡ�ȣ�����С���ӿڴ�������1��ƹ��������ɫ�������ܶ���������ƹ������ɫ��ͬ��������Ӯ������С��Ӯ��
�� ������״ͼ���б��ķ�����ʾ��Ϸ�����п��ܳ��ֵĽ����
�� �����Ϸ�������Ϸ˫����ƽ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
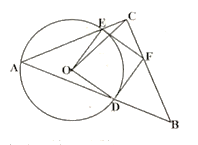
����Ŀ����ͼ������![]() ��һ����Ƕ���
��һ����Ƕ���![]() ��
��![]() �ϵ�һ�����㣬
�ϵ�һ�����㣬![]() ����
����![]() ���
��б��![]() �ֱ�
�ֱ�![]() �ڵ�
�ڵ�![]() ���ֱ����
���ֱ����![]() ��
��![]() �����߽��ڵ�
�����߽��ڵ�![]() ���ҵ�
���ҵ�![]() ǡ������
ǡ������![]() �ϵĵ㣬����
�ϵĵ㣬����![]() ����
����![]() �İ뾶Ϊ4����
�İ뾶Ϊ4����![]() �����ֵΪ���� ��
�����ֵΪ���� ��
A.![]() B.
B.![]() C.6D.8
C.6D.8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
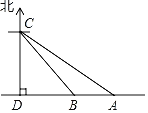
����Ŀ���ݵ��飺������ʻ��������ͨ�¹ʵ���Ҫԭ��֮һ��С������ѧ֪ʶ��һ����ֱ��·�ϳ������в��٣���ͼ��ʾ���۲��C����·�ľ���CD��200m�����·�ε����Aλ�ڵ�C����ƫ��60�㷽���ϣ��յ�Bλ�ڵ�C����ƫ��45�㷽���ϣ�һ���γ��ɶ�����������ʻ����ô˳���A����ʻ��B��ʱ��ʱ��Ϊ10s���ʴ˳��Ƿ��˸�·��10m/s�������ٶȣ����۲��C�����ľ�����Բ��ƣ���ר���ݣ�![]() 1.41��
1.41��![]() 1.73��
1.73��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
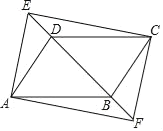
����Ŀ����ͼ����ABCD�У���E��F��ֱ��BD�ϵ����㣬DE=BF��
��1����֤���ı���AFCE��ƽ���ı��Σ�
��2����BD��AD��AB=5��AD=3���ı���AFCE�Ǿ��Σ���DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
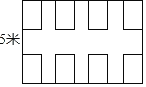
����Ŀ����ͼ��ʾ����һ����5�IJ�����ֻ�ܷ�8�Ų������ּƻ�����������λ��ֻ�ܶ�ԭ���Ƚ��мӳ�����ӳ���ij���Ϊm�ף��������IJ�����Ϊy�������㣬�õ��������ݣ���ע��m��y��Ϊ��������
m���ף� | 5 | 8 | 11 | 14 | ���� |
������y���ţ� | 8 | 12 | 16 | ���� |
��1�����ݱ������ݵĹ��ɣ�������ϱ���
��2�����y����m�ĺ�������ʽ��
��3������Ҳ�������Ҫ��80�Ų�������m����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
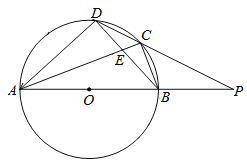
����Ŀ����ͼ,���ı���ABCD�У���ABΪֱ���İ�ԲO������C,D��AC��BD�ཻ�ڵ�E��CD2=CE��CA,�ֱ��ӳ�AB,DC�ཻ�ڵ�P��PB=BO��CD=2![]() ����BO�ij���_________��
����BO�ij���_________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com