
【题目】如图所示,已知正方形ABCD中的△DCF可以经过旋转得到△BCE .
①图中哪一个点是旋转中心?
②按什么方向旋转了多少度?
③如果CF=3cm.求EF的长?
【答案】【解答】①△DCF绕点C逆时针旋转得到△BCE ,
所以旋转中心为点C;
②∵四边形ABCD为正方形,
∴CB=CD , ∠BCD=90°,
∴△DCF绕点C逆时针旋转90°得到△BCE;
③∵△DCF绕点C逆时针旋转90°得到△BCE ,
∴CE=CF , ∠ECF=90°,连接EF
∴△CEF为等腰直角三角形,
∴EF=![]() CF=
CF=![]() cm.
cm.
【解析】①②根据旋转的定义求解;③根据旋转的性质得CE=CF , ∠ECF=90°,则可判断△CEF为等腰直角三角形,然后根据等腰直角三角形的性质求解.
【考点精析】本题主要考查了旋转的性质的相关知识点,需要掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:
【题目】可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相等价格的购物券,购物券可以在本商场消费.某顾客刚好消费300元.
(1)该顾客至多可得到 元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于50元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形的边长为a厘米,如果它的一边长增加3厘米,另一边减少3厘米,那么它的面积( )
A. 不变 B. 减少9平方厘米
C. 增加9平方厘米 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于雾霾天气频发,市场上防护口罩出现热销,某医药公司每月固定生产甲、乙两种型号的防雾霾口罩共20万只,且所有产品当月全部售出,原料成本、销售单价及工人生产提成如表:
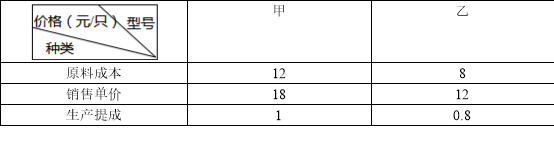
(1)若该公司五月份的销售收入为300万元,求甲、乙两种型号的产品分别是多少万只?
(2)公司实行计件工资制,即工人每生产一只口罩获得一定金额的提成,如果公司六月份投入总成本(原料总成本+生产提成总额)不超过239万元,应怎样安排甲、乙两种型号的产量,可使该月公司所获利润最大?并求出最大利润(利润=销售收入﹣投入总成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着某市养老机构(养老机构指社会福利院、养老院、社区养老中心等)建设稳步推进,拥有的养老床位不断增加.
(1)该市的养老床位数从2013年底的2万个增长到2015年底的2.88万个,求该市这两年(从2013年度到2015年底)拥有的养老床位数的平均年增长率;
(2)若该市某社区今年准备新建一养老中心,其中规划建造三类养老专用房间共100间,这三类养老专用房间分别为单人间(1个养老床位),双人间(2个养老床位),三人间(3个养老床位),因实际需要,单人间房间数在10至30之间(包括10和30),且双人间的房间数是单人间的2倍,设规划建造单人间的房间数为t.
①若该养老中心建成后可提供养老床位200个,求t的值;
②求该养老中心建成后最多提供养老床位多少个?最少提供养老床位多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com