
【题目】如图,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB , 求∠BAB′的度数.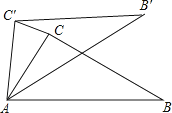
【答案】【解答】∵CC′∥AB ,
∴∠A CC′=∠CAB=70°,
∵△ABC绕点A旋转到△AB′C′的位置,
∴AC=AC′,∠BAB′=∠CAC′,
在△ACC′中,∵AC=AC′
∴∠ACC′=∠AC′C=70°,
∴∠CAC′=180°-70°-70°=40°,
∴∠BAB′=40°.
【解析】先根据平行线的性质,由CC′∥AB得∠ACC′=∠CAB=70°,再根据旋转的性质得AC=AC′,∠BAB′=∠CAC′,于是根据等腰三角形的性质有∠ACC′=∠AC′C=70°,然后利用三角形内角和定理可计算出∠CAC′=40°,从而得到∠BAB′的度数.
【考点精析】解答此题的关键在于理解旋转的性质的相关知识,掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角形的斜边上,AC与DM , DN分别交于点E , F , 把△DEF绕点D旋转到一定位置,使得DE=DF , 则∠BDN的度数是( )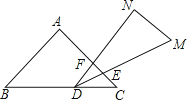
A.105°
B.115°
C.120°
D.135°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知正方形ABCD中的△DCF可以经过旋转得到△BCE .
①图中哪一个点是旋转中心?
②按什么方向旋转了多少度?
③如果CF=3cm.求EF的长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AC=BC , 点D在边AB上,连接CD , 将线段CD绕点C顺时针旋转90°至CE位置,连接AE . 求证:AE=BD . 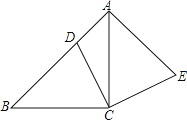
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠1=∠2,G是AD的中点,延长BG交AC于点E,F为AB上一点,CF⊥AD交AD于点H.①AD是△ABE的角平分线;②BE是△ABD的边AD上的中线;③CH为△ACD的边AD上的高;④AH是△ACF的角平分线和高线,其中判断正确的有.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com