
【题目】如图,△ABC中,∠ACB=90°,AC=BC , 点D在边AB上,连接CD , 将线段CD绕点C顺时针旋转90°至CE位置,连接AE . 求证:AE=BD . 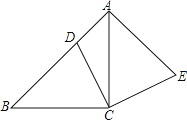
【答案】【解答】
证明:∵线段CD绕点C顺时针旋转90°至CE位置,
∴CD=CE , ∠DCE=90°,
∵CB=CA , ∠BCA=90°,
∴△BCD绕点C顺时针旋转90°得到△ACE ,
∴AE=BD .
【解析】先根据旋转的性质,由线段CD绕点C顺时针旋转90°至CE位置得到CD=CE , ∠DCE=90°,加上CB=CA , ∠BCA=90°,于是根据旋转的定义可把△BCD绕点C顺时针旋转90°得到△ACE , 然后根据旋转的性质即可得到结论.
【考点精析】关于本题考查的旋转的性质,需要了解①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】随着某市养老机构(养老机构指社会福利院、养老院、社区养老中心等)建设稳步推进,拥有的养老床位不断增加.
(1)该市的养老床位数从2013年底的2万个增长到2015年底的2.88万个,求该市这两年(从2013年度到2015年底)拥有的养老床位数的平均年增长率;
(2)若该市某社区今年准备新建一养老中心,其中规划建造三类养老专用房间共100间,这三类养老专用房间分别为单人间(1个养老床位),双人间(2个养老床位),三人间(3个养老床位),因实际需要,单人间房间数在10至30之间(包括10和30),且双人间的房间数是单人间的2倍,设规划建造单人间的房间数为t.
①若该养老中心建成后可提供养老床位200个,求t的值;
②求该养老中心建成后最多提供养老床位多少个?最少提供养老床位多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一根40cm的金属棒,欲将其截成x根7cm的小段和y根9cm的小段,剩余部分作废料处理,若使废料最少,则正整数x,y应分别为( )
A.x=1,y=3 B.x=4,y=1 C.x=3,y=2 D.x=2,y=3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现要利用尺规作图作△ABC关于BC的轴对称图形△A′BC . 若AB=5cm , AC=6cm , BC=7cm , 则分别以点B、C为圆心,依次以cm、cm为半径画弧,使得两弧相交于点A′ , 再连结A′C、A′B , 即可得△A′BC . 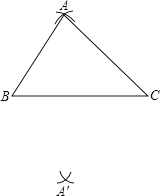
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com