
【题目】随着某市养老机构(养老机构指社会福利院、养老院、社区养老中心等)建设稳步推进,拥有的养老床位不断增加.
(1)该市的养老床位数从2013年底的2万个增长到2015年底的2.88万个,求该市这两年(从2013年度到2015年底)拥有的养老床位数的平均年增长率;
(2)若该市某社区今年准备新建一养老中心,其中规划建造三类养老专用房间共100间,这三类养老专用房间分别为单人间(1个养老床位),双人间(2个养老床位),三人间(3个养老床位),因实际需要,单人间房间数在10至30之间(包括10和30),且双人间的房间数是单人间的2倍,设规划建造单人间的房间数为t.
①若该养老中心建成后可提供养老床位200个,求t的值;
②求该养老中心建成后最多提供养老床位多少个?最少提供养老床位多少个?
【答案】(1)20%;(2)①25;②该养老中心建成后最多提供养老床位260个,最少提供养老床位180个.
【解析】
试题分析:(1)设该市这两年(从2013年度到2015年底)拥有的养老床位数的平均年增长率为x,根据“2015年的床位数=2013年的床位数×(1+增长率)的平方”可列出关于x的一元二次方程,解方程即可得出结论;
(2)①设规划建造单人间的房间数为t(10≤t≤30),则建造双人间的房间数为2t,三人间的房间数为100﹣3t,根据“可提供的床位数=单人间数+2倍的双人间数+3倍的三人间数”即可得出关于t的一元一次方程,解方程即可得出结论;
②设该养老中心建成后能提供养老床位y个,根据“可提供的床位数=单人间数+2倍的双人间数+3倍的三人间数”即可得出y关于t的函数关系式,根据一次函数的性质结合t的取值范围,即可得出结论.
试题解析:(1)设该市这两年(从2013年度到2015年底)拥有的养老床位数的平均年增长率为x,由题意可列出方程:![]()
解得:![]() =0.2=20%,
=0.2=20%,![]() =﹣2.2(不合题意,舍去).
=﹣2.2(不合题意,舍去).
答:该市这两年拥有的养老床位数的平均年增长率为20%.
(2)①设规划建造单人间的房间数为t(10≤t≤30),则建造双人间的房间数为2t,三人间的房间数为100﹣3t,由题意得:t+4t+3(100﹣3t)=200,解得:t=25.
答:t的值是25.
②设该养老中心建成后能提供养老床位y个,由题意得:y=t+4t+3(100﹣3t)=﹣4t+300(10≤t≤30),∵k=﹣4<0,∴y随t的增大而减小.
当t=10时,y的最大值为300﹣4×10=260(个),当t=30时,y的最小值为300﹣4×30=180(个).
答:该养老中心建成后最多提供养老床位260个,最少提供养老床位180个.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
【题目】现有若干张如图1所示的正方形纸片A,B和长方形纸片C.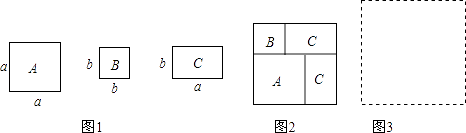
(1)小王利用这些纸片拼成了如图2的一个新正方形,通过用两种不同的方法计算新正方形面积,由此,他得到了一个等式:;
(2)小王再取其中的若干张纸片(三种纸片都要取到)拼成一个面积为a2+3ab+nb2的长方形,则n可取的正整数值是 , 并请你在图3位置画出拼成的长方形;
(3)根据拼图经验,请将多项式a2+5ab+4b2分解因式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算中正确的是( )
A. (x+2)2=x2+2x+4 B. (-3-x)(3+x)=9-x2
C. (-3-x)(3+x)=-x2-9+6x D. (2x-3y)2=4x2+9y2-12xy
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角形的斜边上,AC与DM , DN分别交于点E , F , 把△DEF绕点D旋转到一定位置,使得DE=DF , 则∠BDN的度数是( )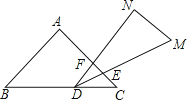
A.105°
B.115°
C.120°
D.135°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=70°,AC=BC , 以点B为旋转中心把△ABC按顺时针旋转α度,得到△A′B′C , 点A′恰好落在AC上,连接CC′,则∠ACC′=.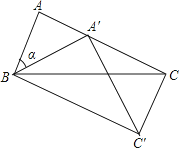
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知正方形ABCD中的△DCF可以经过旋转得到△BCE .
①图中哪一个点是旋转中心?
②按什么方向旋转了多少度?
③如果CF=3cm.求EF的长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AC=BC , 点D在边AB上,连接CD , 将线段CD绕点C顺时针旋转90°至CE位置,连接AE . 求证:AE=BD . 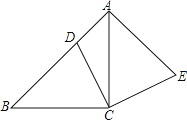
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠1=∠2,G是AD的中点,延长BG交AC于点E,F为AB上一点,CF⊥AD交AD于点H.①AD是△ABE的角平分线;②BE是△ABD的边AD上的中线;③CH为△ACD的边AD上的高;④AH是△ACF的角平分线和高线,其中判断正确的有.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如表所示,从左到右在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,则第2016个格子中的数为( ) ![]()
A.3
B.2
C.0
D.﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com