
分析 将分母中的-2拆开成两个-1,与前面两个平方数分别组成两组平方差公式,因式分解就可便分母与分子能约分.
解答 解:$\frac{2007200{6}^{2}}{2007200{5}^{2}+2007200{7}^{2}-2}$
=$\frac{2007200{6}^{2}}{2007200{5}^{2}-1+2007200{7}^{2}-1}$
=$\frac{2007200{6}^{2}}{20072006×20072004+20072006×20072008}$
=$\frac{2007200{6}^{2}}{20072006×(2004+2008)}$
=$\frac{2007200{6}^{2}}{20072006×20072006×2}$
=$\frac{1}{2}$
点评 本题考查因式分解的应用,属中档题.熟练掌握平方差公式并会拆项是解答本题的关键.


科目:初中数学 来源: 题型:解答题
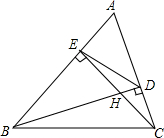 如图,△ABC中,高BD、CE相交于点H,求证:
如图,△ABC中,高BD、CE相交于点H,求证:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com