

分析 (1)由n=1、n=2和n=3时图形中第一行和第一列的数量即可得出答案;
(2)分别清点题目给出的三个图形中的白瓷砖和黑瓷砖的块数,然后通过分析,找出白瓷砖和黑瓷砖的块数与图形数之间的规律,即可解答此题;
(3)根据题意分别列出两种活动中总费用的代数式,再代入求值即可.
解答 解:(1)根据题意知,在第n个图中,第一横行共 n+3块瓷砖,第一竖列共有n+2块瓷砖,
故答案为:n+3,n+2;
(2)通过观察图形可知,当n=1时,用白瓷砖2块,黑瓷砖10块;
当n=2时,用白瓷砖6块,黑瓷砖14块;
当n=3时,用白瓷砖12块,黑瓷砖18块;
可以发现,需要白瓷砖的数量和图形数之间存在这样的关系,即白瓷砖块数等于图形数的平方加上图形数;
需要黑瓷砖的数量和图形数之间存在这样的关系,即黑瓷砖块数等于图形数的4倍加上图形数.
所以,在第n个图形中,白瓷砖的块数可用含n的代数式表示为n2+n;
白瓷砖的块数可用含n的代数式表示为4n+6,
故答案为:4n+6;
(3)原价时,总价=4(4n+6)=16n+24,
活动一:当n=6时,原式=112;
活动二:4(4n+6)×0.9=14.4n+21.6,当n=6时,原式=108,
综合上述,小明参加活动二合算.
点评 本题主要考查图形的变化规律,解决这类问题首先要从简单图形入手,抓住随着“编号”或“序号”增加时,后一个图形与前一个图形相比,在数量上增加(或倍数)情况的变化,找出数量上的变化规律,从而推出一般性的结论.


科目:初中数学 来源: 题型:选择题
| A. | 少100 | B. | 少200 | C. | 多100 | D. | 多200 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
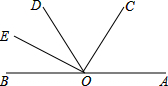 如图,已知AOB是一条直线,OC是∠AOD 的平分线,OE是∠BOD的平分线.
如图,已知AOB是一条直线,OC是∠AOD 的平分线,OE是∠BOD的平分线.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ${3^{-2}}=-\frac{1}{9}$ | B. | ${(-3)^{-2}}=-\frac{1}{9}$ | C. | ${(-\frac{1}{3})^{-2}}=9$ | D. | ${(-\frac{1}{3})^{-2}}=-9$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
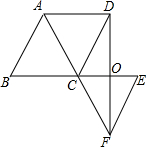 如图,延长?ABCD的边BC至点E,使CE=BC,连接AC并延长至点F,使CF=AC,连接EF、DF,DF交CE于O,求证:OD=OF.
如图,延长?ABCD的边BC至点E,使CE=BC,连接AC并延长至点F,使CF=AC,连接EF、DF,DF交CE于O,求证:OD=OF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com