
分析 先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:原式=$\frac{3x(x+1)-x(x-1)}{(x-1)(x+1)}$•$\frac{x(x+1)(x-1)}{{x}^{2}(x+2)(x-2)}$
=$\frac{2x(x+2)}{(x-1)(x+1)}$•$\frac{(x+1)(x-1)}{x(x+2)(x-2)}$
=$\frac{x}{x-2}$,
当x=$\sqrt{2}$+2时,原式=$\frac{\sqrt{2}+2}{\sqrt{2}+2-2}$=1+$\sqrt{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:选择题
| A. | 不论x为何值,总有y<0 | B. | y随x的增大而减小 | ||
| C. | 图象经过点(1,-3) | D. | 图象经过第二、四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
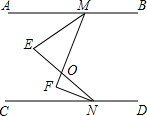 如图,AB∥CD,EM是∠AMF的平分线,NF是∠CNE的平分线,EN、MF交于O点
如图,AB∥CD,EM是∠AMF的平分线,NF是∠CNE的平分线,EN、MF交于O点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com