
【题目】如图,已知A(1,5),直线l1:y=x,直线l2过原点且与x轴正半轴成60°夹角,在l1上有一动点M,在l2上有一动点N,连接AM、MN,则AM+MN的最小值为_____.

【答案】![]()
【解析】
根据“AAS”可证△AOC≌BOD,利用全等三角形对应边相等可得OD=OC=5,BD=AC=1,作NE⊥x轴,BF⊥NE,可得∠BNF=60°,设BN=2x,则NF=x,BF=![]() , 可得OE=OD-DE=5-
, 可得OE=OD-DE=5-![]() , NE =NF+EF=x+1,利用tan∠NOE=
, NE =NF+EF=x+1,利用tan∠NOE=![]() =
=![]() ,解出x的值即可.
,解出x的值即可.
解:如图,做点A关于l1的对称点B,过BN⊥l2,交l1于一点即为M,此时,线段BN的长即为AM+MN的最小值,
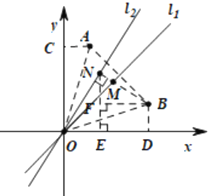
∴AO=BO,
作AC⊥y轴,BD⊥x轴,
易证△AOC≌BOD(AAS),
∵A(1,5)
∴B(5,1)
∴OD=5,BD=1,
作NE⊥x轴,BF⊥NE,
∵直线L2与x轴夹角为60°,
∴∠BNF=60°,
设BN=2x,则NF=x,BF=![]()
∴OE=OD-DE=5-![]() , NE =NF+EF=x+1,
, NE =NF+EF=x+1,
tan∠NOE=![]() =
=![]() =tan60°=
=tan60°=![]() ,
,
解得x=![]() ,
,
∴BN=2x=![]() .
.
即得AM+MN的最小值为![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为3,点E,F分别在射线DC,DA上运动,且DE=DF.连接BF,作EH⊥BF所在直线于点H,连接CH.
(1)如图1,若点E是DC的中点,CH与AB之间的数量关系是 ;
(2)如图2,当点E在DC边上且不是DC的中点时,(1)中的结论是否成立?若成立给出证明;若不成立,说明理由;
(3)如图3,当点E,F分别在射线DC,DA上运动时,连接DH,过点D作直线DH的垂线,交直线BF于点K,连接CK,请直接写出线段CK长的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中国汉字听写大会”是由中央电视台和国家语言文字工作委员会联合主办的节目,希望通过节目的播出,能吸引更多的人关注对汉字文化的学习.某校也开展了一次“汉字听写”比赛,每位参赛学生听写40个汉字.比赛结束后随机抽取部分学生的听写结果,按听写正确的汉字个数x绘制成了以下不完整的统计图.

根据以上信息回答下列问题:
(1)本次共随机抽取了 名学生进行调查,听写正确的汉字个数x在 范围的人数最多;
(2)补全频数分布直方图;
(3)各组的组中值如下表所示.若用各组的组中值代表各组每位学生听写正确的汉字个数,求被调查学生听写正确的汉字个数的平均数;
听写正确的汉字个数x | 组中值 |
1≤x<11 | 6 |
11≤x<21 | 16 |
21≤x<31 | 26 |
31≤x<41 | 36 |
(4)该校共有1350名学生,如果听写正确的汉字个数不少于21个定为良好,请你估计该校本次“汉字听写”比赛达到良好的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校开展的数学活动课上,小明和小刚制作了一个正三楼锥(质量均匀,四个面完全相同),并在各个面上分别标记数字1,2,3,4,游戏规则如下每人投掷三棱锥两次,并记录底面的数字,如果两次所掷数字的和为单数,那么算小明赢,如果两欢所掷数字的和为偶数,那么算小明赢;
(1)请用列表或者面树状围的方法表示上述游戏中的所有可能结果.
(2)请分别隶出小明和小刚能赢的概率,并判新游戏的公平性.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,CD=12m,DA=13m,∠B=90°,连接AC.
(1)△ACD是直角三角形吗?为什么?
(2)小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问铺满这块空地共需花费多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
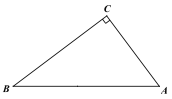
【题目】如图,Rt△ABC,AC⊥CB,AC=15,AB=25,点D为斜边上动点。

(1)如图,过点D作DE⊥AB交CB于点E,连接AE,当AE平分∠CAB时,求CE;

(2)如图,在点D的运动过程中,连接CD,若△ACD为等腰三角形,求AD。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=kx+3和x轴、y轴的交点分别为B、C,∠OBC=30°,点A的坐标是(![]() ,0),另一条直线经过点A、C.
,0),另一条直线经过点A、C.
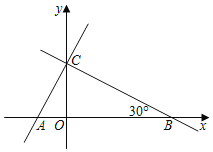
(1)求点B的坐标及k的值;
(2)求证:AC⊥BC;
(3)点M为直线BC上一点(与点B不重合),设点M的横坐标为x,△ABM的面积为S.
①求S与x的函数关系式;
②当S=6![]() 时,求点M的坐标.
时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com