Question

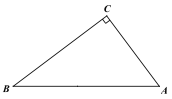
【题目】如图，Rt△ABC，AC⊥CB,AC=15，AB=25,点D为斜边上动点。

（1）如图，过点D作DE⊥AB交CB于点E,连接AE,当AE平分∠CAB时，求CE；

（2）如图，在点D的运动过程中，连接CD，若△ACD为等腰三角形，求AD。

Answer 1

【答案】（1）7.5（2）①15②12.5③18

【解析】

（1）在Rt△ABC中， AC=15，AB=25，由勾股定理得BC=20，根据角平分线的性质得DE=DC，证得△ACE≌△AED，AD=AC=15， BD=25-15=10，设CE=x,则BE=20-x，在在Rt△BED中，由勾股定理得 ，解得x=7.5，即CE=7.5.（2）若△ACD为等腰三角形，分三种情况，即CD=AC、CD=AD或AD=AC，利用等腰三角形的三线合一性质和三角形面积即可解答，难度不大.

(1) ∵AC⊥CB,AC=15，AB=25

∴BC=20

∵AE平分∠CAB

∴∠EAC=∠EAD

∵AC⊥CB, DE⊥AB

∴∠EDA=∠ECA=90°

∵AE=AE

∴△ACE≌△AED

∴CE=DE,AC=AD=15

设CE=x,则BE=20-x,BD=25-15=10

在Rt△BED中

∴

∴x=7.5

∴CE=7.5

(2) ①当AD=AC时，△ACD为等腰三角形

∵AC=15 ∴AD=AC=15

②当CD=AD时，△ACD为等腰三角形

∵CD=AD

∴∠DCA=∠CAD

∵∠CAB+∠B=90°

∠DCA+∠BCD=90°

∴∠B=∠BCD

∴BD=CD

∴CD=BD=DA=12.5

③当CD=AC时，△ACD为等腰三角形

如图，作CH⊥BA于点H,

则

∵AC=15，BC=20，AB=25

∴CH=12

在Rt△ACH中，易求AH=9

∵CD=AC , CH⊥BA

∴DH=HA=9

∴AD=18