
【题目】已知△ABC为等边三角形,D为直线AC上一点,延长BC至E,使CE=AD,联结BD,DE.

(1)如图(a),当D为边AC的中点时,求证:△BDE为等腰三角形.
(2)如图(b),当点D在边AC上,但不是边AC的中点时,△BDE还是等腰三角形吗?如果是,请给予证明;如果不是,说明理由.
(3)当点D在边AC的延长线上时,在图(c)中画出相应的图形,△BDE还是等腰三角形吗?请直接写出结论,不必证明.
【答案】(1)见解析;(2)△BDE还是等腰三角形,理由见解析;(3)△BDE还是等腰三角形,见解析.
【解析】
(1)根据等边三角形的性质得∠ABC=∠ACB=60°,由DA=DC,CE=AD可得CD=CE,推出∠E=∠CDE,再利用∠DCB=∠E+∠CDE=60°得到∠E=30°,根据等边三角形性质得∠DBC=![]() ∠ABC=30°,故可得△BDE为等腰三角形;
∠ABC=30°,故可得△BDE为等腰三角形;
(2)作DM∥BC交AB于M,根据等边三角形的性质得∠A=∠ABC=∠ACB=60°,AB=AC,则∠DCE=120°,由DM∥BC得∠AMD=60°,易得△AMD为等边三角形,则AD=DM=AM,而AD=CE,则DM=EC,然后推出MB=DC,利用“SAS”可判断△BMD≌△DCE,则BD=DE,即可得到 △BDE为等腰三角形;
(3)作DM∥BC交AB的延长线于M,易证△AMD为等边三角形,则AM=AD=MD,∠M=60°,可得到BM=CD,而AD=CE,所以MD=CE,加上∠M=∠ECD=60°,于是可根据“SAS”判断△BMD≌△DCE,则BD=DE,即可得到 △BDE为等腰三角形.
(1)证明:∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,
∵DA=DC,CE=AD,
∴CD=CE,
∴∠E=∠CDE,
而∠DCB=∠E+∠CDE=60°,
∴∠E=30°,
∵∠DBC=![]() ∠ABC=30°,
∠ABC=30°,
∴DB=DE,
∴△BDE为等腰三角形;
(2)△BDE为等腰三角形仍然成立.
理由如下:作DM∥BC交AB于M,如图2,

∵△ABC为等边三角形,
∴∠A=∠ABC=∠ACB=60°,AB=AC,
∴∠DCE=120°,
∵DM∥BC,
∴∠AMD=60°,
∴∠BMD=120°,△AMD为等边三角形,
∴AD=DM=AM,
∵AD=CE,
∴DM=EC,
∴ABAM=ACAD,
∴MB=DC,
在△BMD和△DCE中

∴△BMD≌△DCE(SAS),
∴BD=DE,
∴△BDE为等腰三角形;
(3)△BDE还是等腰三角形.
理由如下:
如图3,作DM∥BC交AB的延长线于M,

易证△AMD为等边三角形,
∴AM=AD=MD,∠M=60°,
∴AB=AC,
∴BM=CD,
∵AD=CE,
∴MD=CE,
∵∠ECD=∠ACB=60°,
∴∠M=∠ECD
在△BMD和△DCE中

∴△BMD≌△DCE(SAS),
∴BD=DE,
∴△BDE为等腰三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
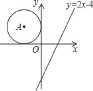
【题目】如图,在平面直角坐标系中,点A在第二象限,⊙A分别与x轴、y轴相切.若将⊙A向右平移5个单位,圆心A恰好落在直线y=2x﹣4上,则⊙A的半径为( )
A. ![]() B. 2 C. 4 D. 6
B. 2 C. 4 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以线段AB两端点A,B为圆心,以大于![]() AB长为半径画弧,两弧交于C,D两点,作直线CD交AB于点M,DE∥AB,BE∥CD.
AB长为半径画弧,两弧交于C,D两点,作直线CD交AB于点M,DE∥AB,BE∥CD.
(1)判断四边形ACBD的形状,并说明理由;
(2)求证:ME=AD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,则下列条件中,不能使△ABC≌△DBC成立的是 ( )

A. AB=CD B. AC=BD C. ∠A=∠D D. ∠ABC=∠DCB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为3,点E,F分别在射线DC,DA上运动,且DE=DF.连接BF,作EH⊥BF所在直线于点H,连接CH.
(1)如图1,若点E是DC的中点,CH与AB之间的数量关系是 ;
(2)如图2,当点E在DC边上且不是DC的中点时,(1)中的结论是否成立?若成立给出证明;若不成立,说明理由;
(3)如图3,当点E,F分别在射线DC,DA上运动时,连接DH,过点D作直线DH的垂线,交直线BF于点K,连接CK,请直接写出线段CK长的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学进行长跑训练,甲和乙所跑的路程S(单位:米)与所用时间t(单位:秒)之间的函数图象分别为线段OA和折线OBCD.则下列说法正确的是( )

A. 两人从起跑线同时出发,同时到达终点
B. 跑步过程中,两人相遇一次
C. 起跑后160秒时,甲、乙两人相距最远
D. 乙在跑前300米时,速度最慢
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠A>∠B,分别以点A,C为圆心,大于![]() AC长为半径画弧,两弧交于点P,点Q,作直线PQ交AB于点D,再分别以点B,D为圆心,大于
AC长为半径画弧,两弧交于点P,点Q,作直线PQ交AB于点D,再分别以点B,D为圆心,大于![]() BD长为半径画弧,两弧交于点M,点N,作直线MN交BC于点E,若△CDE是等边三角形,则∠A=_____.
BD长为半径画弧,两弧交于点M,点N,作直线MN交BC于点E,若△CDE是等边三角形,则∠A=_____.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=Rt∠,AC=8cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm,设运动的时间为t秒。

(1)当t为何值时,CP把△ABC的周长分成相等的两部分。
(2)当t为何值时,CP把△ABC的面积分成相等的两部分,并求出此时CP的长;
(3)当t为何值时,△BCP为等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
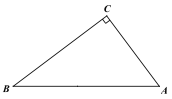
【题目】如图,Rt△ABC,AC⊥CB,AC=15,AB=25,点D为斜边上动点。

(1)如图,过点D作DE⊥AB交CB于点E,连接AE,当AE平分∠CAB时,求CE;

(2)如图,在点D的运动过程中,连接CD,若△ACD为等腰三角形,求AD。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com