
【题目】已知,如图,抛物线y=ax2+bx+c(a≠0)的顶点为M(1,9),经过抛物线上的两点A(﹣3,﹣7)和B(3,m)的直线交抛物线的对称轴于点C.
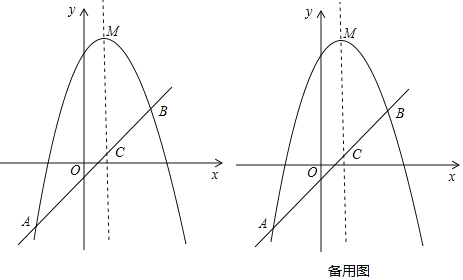
(1)求抛物线的解析式及点B的坐标.
(2)在抛物线上A,M两点之间的部分(不包含A,M两点),是否存在点D,使得S△DAC=2S△DCM?若存在,求出点D的坐标;若不存在,请说明理由.
(3)上下平移直线AB,设平移后的直线与抛物线交与A′,B′两点(A′在左边,B'在右边),且与y轴交与点P(0,n),若∠A′MB′=90°,求n的值.
【答案】(1)y=﹣x2+2x+8,B(3,5);(2)存在,点D(﹣1,5);(3)n=3
【解析】
(1)抛物线的表达式为:y=a(x﹣1)2+9,将点A的坐标代入上式并解得:a=﹣1,即可求解;
(2)S△DAC=2S△DCM,则HN=2GH,即1﹣k﹣(3k﹣7)=2(9﹣k﹣1+k),即可求解;
(3)∠GA′M=∠HMB′,故tan∠GA′M=tan∠HMB′,即:![]() ,而x1+x2=0,x1x2=n﹣8,y1+y2=2n,y1y2=4n﹣32+n2,即可求解.
,而x1+x2=0,x1x2=n﹣8,y1+y2=2n,y1y2=4n﹣32+n2,即可求解.
解:(1)抛物线的表达式为:y=a(x﹣1)2+9,
将点A的坐标代入上式并解得:a=﹣1,
故抛物线的表达式为:y=﹣x2+2x+8,
将点B坐标代入上式并解得:m=5,
故点B(3,5);
(2)过点M、C、A分别作三条相互平移的平行线,分别交y轴于点G、H、N,直线l与抛物线交于点D,
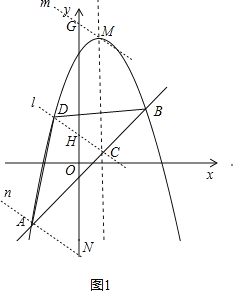
设直线m的表达式为:y=kx+t,将点M的坐标代入上式并解得:t=9﹣k,
故直线m的表达式为:y=kx+9﹣t,即点G(0,9﹣t),
同理直线l的表达式为:y=kx+1﹣k,故点H(0,1﹣k),
同理直线n的表达式为:y=kx+3k﹣7,故点N(0,3k﹣7),
S△DAC=2S△DCM,则HN=2GH,
即1﹣k﹣(3k﹣7)=2(9﹣k﹣1+k),
解得:k=﹣2,
故直线l的表达式为:y=﹣2x+3…②,
联立①②并解得:x=5(舍去)或﹣1,
故点D(﹣1,5);
(3)直线A′B′的表达式为:y=2x+n,
设点A′、B′的坐标分别为:(x1,y1)、(x2,y2),
将抛物线与直线A′B′的表达式联立并整理得:
x2+n﹣8=0,
故x1+x2=0,x1x2=n﹣8,
y1+y2=2(x1+x2)+2n=2n,同理可得:y1y2=4n﹣32+n2,
过点M作x轴的平行线交过点A′与y轴的平行线于点G,交过点B′与y轴的平行线于点H,
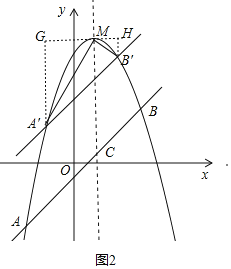
∵∠A′MB′=90°,
∴∠GMA′+∠GA′M=90°,∠GMA′+∠MHB′=90°,
∴∠GA′M=∠HMB′,故tan∠GA′M=tan∠HMB′,
即:![]() ,
,
而x1+x2=0,x1x2=n﹣8,y1+y2=2n,y1y2=4n﹣32+n2,
整理得:n2﹣13n+30=0,
解得:n=3或10(舍去10),
故n=3.


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论中错误的是( )
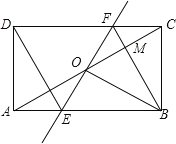
A.FB垂直平分OCB.DE=EF
C.S△AOE:S△BCM=3:2D.△EOB≌△CMB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,张老师举了下面的例题:
例1 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.(答案:
的度数.(答案:![]() )
)
例2 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.(答案:
的度数.(答案:![]() 或
或![]() 或
或![]() )
)
张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.
的度数.
(1)请你解答以上的变式题.
(2)解(1)后,小敏发现,![]() 的度数不同,得到
的度数不同,得到![]() 的度数的个数也可能不同.如果在等腰三角形
的度数的个数也可能不同.如果在等腰三角形![]() 中,设
中,设![]() ,当
,当![]() 有三个不同的度数时,请你探索
有三个不同的度数时,请你探索![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线C1:y=ax2+bx﹣1经过点A(﹣2,1)和点B(﹣1,﹣1),抛物线C2:y=2x2+x+1,动直线x=t与抛物线C1交于点N,与抛物线C2交于点M.
(1)求抛物线C1的表达式;
(2)直接用含t的代数式表达线段MN的长;
(3)当△AMN是以MN为直角边的等腰直角三角形时,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AE与BF相交于点D,AB⊥AE,垂足为点A,EF⊥AE,垂足为点E,点C在AD上,连接BC,要计算A、B两地的距离,甲、乙、丙、丁四组同学分别测量了部分线段的长度和角的度数,各组分别得到以下数据:
甲:AC、∠ACB;
乙:EF、DE、AD;
丙:AD、DE和∠DCB;
丁:CD、∠ABC、∠ADB.
其中能求得A、B两地距离的数据有( )
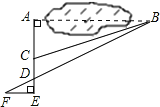
A.甲、乙两组B.丙、丁两组
C.甲、乙、丙三组D.甲、乙、丁三组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,防洪大堤的横断面是梯形,背水坡AB的坡比i=1:![]() ,且AB=30m,李亮同学在大堤上A点处用高1.5m的测量仪测出高压电线杆CD顶端D的仰角为30°,己知地面BC宽30m,求高压电线杆CD的高度(结果保留三个有效数字,
,且AB=30m,李亮同学在大堤上A点处用高1.5m的测量仪测出高压电线杆CD顶端D的仰角为30°,己知地面BC宽30m,求高压电线杆CD的高度(结果保留三个有效数字,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场第一次用![]() 元购进某款智能清洁机器人进行销售,很快销售一空,商家又用
元购进某款智能清洁机器人进行销售,很快销售一空,商家又用![]() 元第二次购进同款智能清洁机器人,所购进数量是第一次的
元第二次购进同款智能清洁机器人,所购进数量是第一次的![]() 倍,但单价贵了
倍,但单价贵了![]() 元.
元.
(1)求该商家第一次购进智能清洁机器人多少台?
(2)若所有智能清洁机器人都按相同的标价销售,要求全部销售完毕的利润率不低于![]() (不考虑其它因素),那么每台智能清洁机器人的标价至少是多少元?
(不考虑其它因素),那么每台智能清洁机器人的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品每天的销售利润![]() 元,销售单价
元,销售单价![]() 元,间满足函数关系式:
元,间满足函数关系式:![]() ,其图象如图所示.
,其图象如图所示.
(1)销售单价为多少元时,该种商品每天的销售利润最大? 最大利润为多少元?
(2)销售单价在什么范围时,该种商品每天的销售利润不低于21 元?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com