
【题目】某商场第一次用![]() 元购进某款智能清洁机器人进行销售,很快销售一空,商家又用
元购进某款智能清洁机器人进行销售,很快销售一空,商家又用![]() 元第二次购进同款智能清洁机器人,所购进数量是第一次的
元第二次购进同款智能清洁机器人,所购进数量是第一次的![]() 倍,但单价贵了
倍,但单价贵了![]() 元.
元.
(1)求该商家第一次购进智能清洁机器人多少台?
(2)若所有智能清洁机器人都按相同的标价销售,要求全部销售完毕的利润率不低于![]() (不考虑其它因素),那么每台智能清洁机器人的标价至少是多少元?
(不考虑其它因素),那么每台智能清洁机器人的标价至少是多少元?
【答案】(1)20台;(2)1360元
【解析】
(1)设该商家第一次购进机器人x个,根据“第一次用22000元购进某款智能清洁机器人,用48000元第二次购进同款机器人,所购进数量是第一次的2倍,但单价贵了10元”列出方程并解答;
(2)设每个机器人的标价是a元.根据“全部销售完毕的利润率不低于20%”列出不等式并解答.
(1)设该商家第一次购进智能清洁机器人![]() 台
台
依题意,得![]()
![]()
![]() ,
,
经检验:![]() 是原方程的解.
是原方程的解.
答:该商家第一次购进智能清洁机器人200台
(2)设每台智能清洁机器人的标价![]() 元,
元,
两次购进智能清洁机器人:![]() 台,
台,
两次购进智能清洁机器人总进价:![]() 元,
元,
依题意,得![]() ,
,
解得![]() ,
,
答:每台智能清洁机器人的标价至少为140元.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】小华和小峰是两名自行车爱好者,小华的骑行速度比小峰快![]() 两人准备在周长为250米的赛道上进行一场比赛
两人准备在周长为250米的赛道上进行一场比赛![]() 若小华在小峰出发15秒之后再出发,图中
若小华在小峰出发15秒之后再出发,图中![]() 、
、![]() 分别表示两人骑行路程与时间的关系.
分别表示两人骑行路程与时间的关系.
![]() 小峰的速度为______米
小峰的速度为______米![]() 秒,他出发______米后,小华才出发;
秒,他出发______米后,小华才出发;
![]() 小华为了能和小峰同时到达终点,设计了两个方案,方案一:加快骑行速度;方案二:比预定时间提前出发.
小华为了能和小峰同时到达终点,设计了两个方案,方案一:加快骑行速度;方案二:比预定时间提前出发.
![]() 图______
图______![]() 填“A“”或“B“
填“A“”或“B“![]() 代表方案一;
代表方案一;
![]() 若采用方案二,小华必须在小峰出发多久后开始骑行?求出此时小华骑行的路程与时间的函数关系式.
若采用方案二,小华必须在小峰出发多久后开始骑行?求出此时小华骑行的路程与时间的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,DE分别是边AB、AC上的点,且AD=CE,则∠ADC+∠BEA=( )
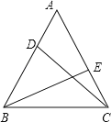
A.180°B.170°C.160°D.150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;(2)AB=BC+AD.
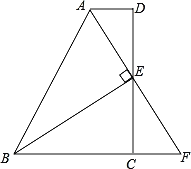
查看答案和解析>>
科目:初中数学 来源: 题型:
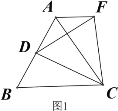
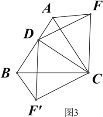
【题目】操作发现:如图1,D是等边△ABC边BA上的一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF,易证AF=BD(不需要证明);
类比猜想:①如图2,当动点D运动至等边△ABC边BA的延长线上时,其它作法与图1相同,猜想AF与BD在图1中的结论是否仍然成立。
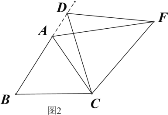
深入探究:②如图3,当动点D在等边△ABC边BA上的一动点(点D与点B不重合),连接DC,以DC为边在BC上方、下方分别作等边△DCF和等边△DCF′,连接AF,BF′你能发现AF,BF′与AB有何数量关系,并证明你发现的结论。
③如图4,当动点D运动至等边△ABC边BA的延长线上时,其它作法与图3相同,猜想AF,BF′与AB在上题②中的结论是否仍然成立,若不成立,请给出你的结论并证明。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰直角三角形ABC中,∠ACB=90°,BC=m,将边AB绕点B顺时针旋转90°得到线段BD,过点D作DE⊥CB交CB的延长线于点E,连接CD.
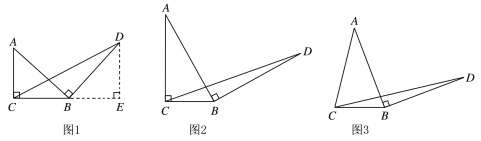
(1)直接写出△BCD的面积为 (用含m的式子表示).
(2)如图2,在一般的Rt△ABC中,∠ACB=90°,BC=m,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,用含m的式子表示△BCD的面积,并说明理由.
(3)如图3,在等腰△ABC中,AB=AC,BC=8,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,则△BCD的面积为 ;若BC=m,则△BCD的面积为 (用含m的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A、C的坐标分别为A(﹣3,0),C(1,0),tan∠BAC=![]() .
.

(1)求点B的坐标;
(2)在x轴上找一点D,连接BD使得△ABD与△ABC相似(不包括全等),并求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点P是BC延长线上一点,连结PD并延长交BA延长线于点E.记△ABP的面积为S1,△ECP的面积为S2,则S1与S2的大小关系是( )
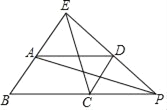
A. S1=S2 B. S1>S2 C. S1<S2 D. 都可能
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的钢架中,∠A=18°,焊上等长的钢条P1P2,P2P3,P3P4,P4P5…来加固钢架.∠P5P4B的度数是( )
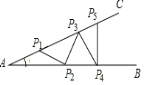
A.80°B.85°C.90°D.100°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com