
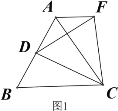
【题目】操作发现:如图1,D是等边△ABC边BA上的一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF,易证AF=BD(不需要证明);
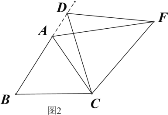
类比猜想:①如图2,当动点D运动至等边△ABC边BA的延长线上时,其它作法与图1相同,猜想AF与BD在图1中的结论是否仍然成立。
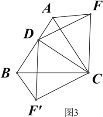
深入探究:②如图3,当动点D在等边△ABC边BA上的一动点(点D与点B不重合),连接DC,以DC为边在BC上方、下方分别作等边△DCF和等边△DCF′,连接AF,BF′你能发现AF,BF′与AB有何数量关系,并证明你发现的结论。
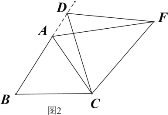
③如图4,当动点D运动至等边△ABC边BA的延长线上时,其它作法与图3相同,猜想AF,BF′与AB在上题②中的结论是否仍然成立,若不成立,请给出你的结论并证明。

【答案】①成立,证明见详解;②AF+BF′=AB,证明见详解;③不成立,AF=AB+BF′,证明见详解.
【解析】
类比猜想:①通过证明△BCD≌△ACF,即可证明AF=BD;
深入探究:②AF+BF′=AB,利用全等三角形△BCD≌△ACF(SAS)的对应边BD=AF;同理△BCF′≌△ACD(SAS),则BF′=AD,所以AF+BF′=AB;
③结论不成立.新的结论是AF=AB+BF′;通过证明△BCF′≌△ACD(SAS),则BF′=AD(全等三角形的对应边相等);再结合(2)中的结论即可证得AF=AB+BF′.
解:类比猜想:①如图2中,
∵△ABC是等边三角形(已知),
∴BC=AC,∠BCA=60°(等边三角形的性质);
同理知,DC=CF,∠DCF=60°;
∴∠BCA+∠DCA=∠DCF+∠DCA,即∠BCD=∠ACF;
在△BCD和△ACF中,
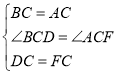
∴△BCD≌△ACF(SAS),
∴BD=AF(全等三角形的对应边相等);
深入探究:②如图示
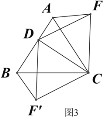
AF+BF′=AB;
证明如下:由①条件可知:∠BCA-∠DCA=∠DCF-∠DCA,即∠BCD=∠ACF,
∴同理可证△BCD≌△ACF(SAS),则BD=AF;
同理△BCF′≌△ACD(SAS),则BF′=AD,
∴AF+BF′=BD+AD=AB;
③结论不成立.新的结论是AF=AB+BF′;
如图示:
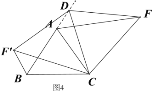
证明如下:
∵等边△DCF和等边△DCF′,由①同理可知:
在△BCF′和△ACD中,
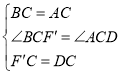
∴△BCF′≌△ACD(SAS),
∴BF′=AD(全等三角形的对应边相等);
又由②知,AF=BD;
∴AF=BD=AB+AD=AB+BF′,即AF=AB+BF′.


科目:初中数学 来源: 题型:
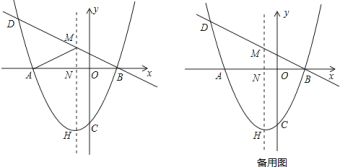
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,顶点为
,顶点为![]() ,其对称轴交
,其对称轴交![]() 轴于点
轴于点![]() .直线
.直线![]() 经过
经过![]() 、
、![]() 两点,交抛物线的对称轴于点
两点,交抛物线的对称轴于点![]() ,其中点
,其中点![]() 的横坐标为
的横坐标为![]() .
.
(1)求抛物线的表达式;
(2)连接![]() ,求
,求![]() 的周长;
的周长;
(3)若![]() 是抛物线位于直线
是抛物线位于直线![]() 的下方且在其对称轴左侧上的一点,当四边形
的下方且在其对称轴左侧上的一点,当四边形![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了创建书香校园,去年又购进了一批图书.经了解,科普书的单价比文学书的单价多4元,用1200元购进的科普书与用800元购进的文学书本数相等.
(1)求去年购进的文学羽和科普书的单价各是多少元?
(2)若今年文学书和科普书的单价和去年相比保持不变,该校打算用1000元再购进一批文学书和科普书,问购进文学书55本后至多还能购进多少本科普书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题探究)小敏在学习了Rt△ABC的性质定理后,继续进行研究.
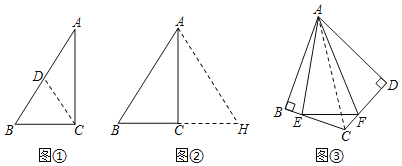
(1)(i)她发现图①中,如果∠A=30°,BC与AB存在特殊的数量关系是 ;
(ii)她将△ABC沿AC所在的直线翻折得△AHC,如图②,此时她证明了BC和AB的关系;请根据小敏证明的思路,补全探究的证明过程;
猜想:如果∠A=30°,BC与AB存在特殊的数量关系是 ;
证明:△ABC沿AC所在的直线翻折得△AHC,
(2)如图③,点E、F分别在四边形ABCD的边BC、CD上,且∠B=∠D=90°,连接AE、AF、EF,将△ABE、△ADF折叠,折叠后的图形恰好能拼成与△AEF完全重合的三角形,连接AC,若∠EAF=30°,AB2=27,则△CEF的周长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成,需支付运费4800元.已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少200元.
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟?
(2)若单独租用一台车,租用哪台车合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场第一次用![]() 元购进某款智能清洁机器人进行销售,很快销售一空,商家又用
元购进某款智能清洁机器人进行销售,很快销售一空,商家又用![]() 元第二次购进同款智能清洁机器人,所购进数量是第一次的
元第二次购进同款智能清洁机器人,所购进数量是第一次的![]() 倍,但单价贵了
倍,但单价贵了![]() 元.
元.
(1)求该商家第一次购进智能清洁机器人多少台?
(2)若所有智能清洁机器人都按相同的标价销售,要求全部销售完毕的利润率不低于![]() (不考虑其它因素),那么每台智能清洁机器人的标价至少是多少元?
(不考虑其它因素),那么每台智能清洁机器人的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC,DC⊥BC,E是BC上一点,使得AE⊥DE;
(1)求证:△ABE∽△ECD;
(2)若AB=4,AE=BC=5,求CD的长;
(3)当△AED∽△ECD时,请写出线段AD、AB、CD之间数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BD,CE分别是AC,AB边上的高,BD, CE交于O,则图中共有相似三角形( )
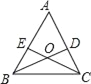
A. 5对 B. 6对 C. 7对 D. 8对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一扇窗户垂直打开,即OM⊥OP,AC是长度不变的滑动支架,其中一端固定在窗户的点A处,另一端在OP上滑动,将窗户OM按图示方向内旋转35°到达ON位置,此时点A,C的对应位置分别是点B,D,测量出∠ODB=25°,点D到点O的距离为30cm,求滑动支架BD的长.
(结果精确到1cm,参考数据:sin25°≈0.42,cos25°≈0.91,tan25°≈0.47,sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com