
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,顶点为
,顶点为![]() ,其对称轴交
,其对称轴交![]() 轴于点
轴于点![]() .直线
.直线![]() 经过
经过![]() 、
、![]() 两点,交抛物线的对称轴于点
两点,交抛物线的对称轴于点![]() ,其中点
,其中点![]() 的横坐标为
的横坐标为![]() .
.
(1)求抛物线的表达式;
(2)连接![]() ,求
,求![]() 的周长;
的周长;
(3)若![]() 是抛物线位于直线
是抛物线位于直线![]() 的下方且在其对称轴左侧上的一点,当四边形
的下方且在其对称轴左侧上的一点,当四边形![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标.
的坐标.
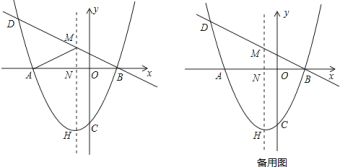
【答案】(1)抛物线的解析式为![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)将A,B两点的坐标代入抛物线的解析式即可求出.
(2)首先求出D点、A点、B点坐标,进而利用待定系数法求出直线DB的解析式,再利用勾股定理得出BM的长,即可得出△ABM的周长;
(3)首先表示出P,Q点的坐标,进而表示出S四边形DPHM=S△DPM+S△PMH,利用二次函数最值求出即可
![]() 将
将![]() ,
,![]() 点坐标代入解析式,得
点坐标代入解析式,得
![]() ,
,
解得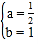 ,
,
抛物线的解析式为![]() ;
;
![]() 当
当![]() ,
,![]() ,则
,则![]() .
.
由![]() ,
,![]() ,
,
则![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
则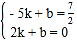 ,
,
解得: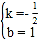 ,
,
则直线![]() 的解析式为
的解析式为![]() ,
,
抛物线对称轴为![]() ,则
,则![]()
在![]() 中,
中,![]() ,
,
∴![]() ,
,
![]() 垂直平分
垂直平分![]() ,则
,则![]() ,
,
则![]() ,
,
所以![]() 的周长为:
的周长为:![]() ;
;
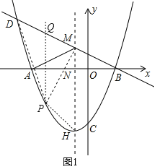
![]() 如图
如图![]() ,连接
,连接![]() ,过
,过![]() 作
作![]() 垂直于
垂直于![]() 轴交
轴交![]() 于
于![]()
抛物线的顶点坐标![]() 为
为![]()
令![]() ,则
,则![]() ,
,
则![]() ,
,
![]() ,
,
![]() ,
,
故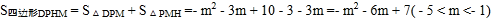
∵![]() ,
,
∴抛物线开口向下,
故当![]() 时,
时,![]() 最大,则
最大,则![]() ,
,
则![]() .
.


 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 在
在![]() 的
的![]() 边上,
边上,![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() ,若添加条件________,则四边形
,若添加条件________,则四边形![]() 是矩形;若添加条件________,则四边形
是矩形;若添加条件________,则四边形![]() 是菱形;若添加条件________,则四边形
是菱形;若添加条件________,则四边形![]() 是正方形.
是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,点
的位置,点![]() 、
、![]() 分别落在点
分别落在点![]() 、
、![]() 处,点
处,点![]() 在
在![]() 轴上,再将
轴上,再将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,点
的位置,点![]() 在
在![]() 轴上,将
轴上,将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,点
的位置,点![]() 在
在![]() 轴上,依次进行下去….若点
轴上,依次进行下去….若点![]() ,
,![]() ,则点
,则点![]() 的坐标为( )
的坐标为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【题目】如图,已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,且经
,且经![]() 、
、![]() 两点.
两点.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 在抛物线的对称轴
在抛物线的对称轴![]() 上,是否存在点
上,是否存在点![]() ,使它到点
,使它到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小,如果存在求出点
的距离之和最小,如果存在求出点![]() 的坐标,如果不存在请说明理由.
的坐标,如果不存在请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华和小峰是两名自行车爱好者,小华的骑行速度比小峰快![]() 两人准备在周长为250米的赛道上进行一场比赛
两人准备在周长为250米的赛道上进行一场比赛![]() 若小华在小峰出发15秒之后再出发,图中
若小华在小峰出发15秒之后再出发,图中![]() 、
、![]() 分别表示两人骑行路程与时间的关系.
分别表示两人骑行路程与时间的关系.
![]() 小峰的速度为______米
小峰的速度为______米![]() 秒,他出发______米后,小华才出发;
秒,他出发______米后,小华才出发;
![]() 小华为了能和小峰同时到达终点,设计了两个方案,方案一:加快骑行速度;方案二:比预定时间提前出发.
小华为了能和小峰同时到达终点,设计了两个方案,方案一:加快骑行速度;方案二:比预定时间提前出发.
![]() 图______
图______![]() 填“A“”或“B“
填“A“”或“B“![]() 代表方案一;
代表方案一;
![]() 若采用方案二,小华必须在小峰出发多久后开始骑行?求出此时小华骑行的路程与时间的函数关系式.
若采用方案二,小华必须在小峰出发多久后开始骑行?求出此时小华骑行的路程与时间的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“互联网+”时代的到来,传统的教学模式也在悄然发生着改变.某出国培训机构紧跟潮流,对培训课程采取了线上线下同步销售的策路,为了让客户更理性的选择,该机构推出了甲、乙两个课程体验包:甲课程体验包价值660元含3节线上课程和2节线下课;乙课程体验包价值990元含2节线上课程和5节线下课程.
(1)分别求出该机构每节课的线上价格和线下价格;
(2)该机构其中一个销售团队上个月的销售业绩为:线上课程成交900节,线下课成交1000节.为回馈客户,本月该机构针对线上、线下每节课程的价格均作出了调整:每节课线上价格比上个月的价格下调a%,线下价格比上个月的价格下调![]() a%,到本月底统计发现,该销售团队线上成交的课程数比上个月增加了
a%,到本月底统计发现,该销售团队线上成交的课程数比上个月增加了![]() a%,线下成交的课程数上升到1080节,最终团队的月销售总额线上比线下少了54000元,求a的值.
a%,线下成交的课程数上升到1080节,最终团队的月销售总额线上比线下少了54000元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小泽和小帅两同学分别从甲地出发,骑自行车沿同一条路到乙地参加社会实践活动.如图折线OAB和线段CD分别表示小泽和小帅离甲地的距离y(单位:千米)与时间x(单位:小时)之间函数关系的图象.根据图中提供的信息,解答下列问题:
(1)小帅的骑车速度为 千米/小时;点C的坐标为 ;
(2)求线段AB对应的函数表达式;
(3)当小帅到达乙地时,小泽距乙地还有多远?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作发现:如图1,D是等边△ABC边BA上的一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF,易证AF=BD(不需要证明);
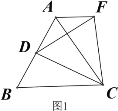
类比猜想:①如图2,当动点D运动至等边△ABC边BA的延长线上时,其它作法与图1相同,猜想AF与BD在图1中的结论是否仍然成立。
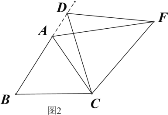
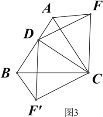
深入探究:②如图3,当动点D在等边△ABC边BA上的一动点(点D与点B不重合),连接DC,以DC为边在BC上方、下方分别作等边△DCF和等边△DCF′,连接AF,BF′你能发现AF,BF′与AB有何数量关系,并证明你发现的结论。
③如图4,当动点D运动至等边△ABC边BA的延长线上时,其它作法与图3相同,猜想AF,BF′与AB在上题②中的结论是否仍然成立,若不成立,请给出你的结论并证明。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com