
ĄŸÌâÄżĄżËæŚĆĄ°»„ÁȘÍű+Ą±Ê±Žú”Ä”œÀŽŁŹŽ«Íł”ÄœÌŃ§ÄŁÊœÒČÔÚÇÄÈ»·ąÉúŚĆžÄ±äŁźÄłłöčúĆàŃ”»úččœôžúł±ÁśŁŹ¶ÔĆàŃ”żÎłÌČÉÈĄÁËÏßÉÏÏßÏÂÍŹČœÏúÊÛ”ÄČß·ŁŹÎȘÁËÈÿͻ§žüÀíĐÔ”ÄŃĄÔńŁŹžĂ»úččÍÆłöÁËŒŚĄąÒÒÁœžöżÎłÌÌćŃé°üŁșŒŚżÎłÌÌćŃé°üŒÛÖ”660ÔȘșŹ3œÚÏßÉÏżÎłÌșÍ2œÚÏßÏ¿Σ»ÒÒżÎłÌÌćŃé°üŒÛÖ”990ÔȘșŹ2œÚÏßÉÏżÎłÌșÍ5œÚÏßÏÂżÎłÌŁź
Łš1Ł©·Ö±đÇółöžĂ»úččĂżœÚżÎ”ÄÏßÉό۞ńșÍÏßÏŒ۞ńŁ»
Łš2Ł©žĂ»úččÆäÖĐÒ»žöÏúÊÛÍƶÓÉÏžöÔ”ÄÏúÊÛÒ”ŒšÎȘŁșÏßÉÏżÎłÌłÉœ»900œÚŁŹÏßÏÂżÎłÉœ»1000œÚŁźÎȘ»ŰÀĄżÍ»§ŁŹ±ŸÔžûúččŐë¶ÔÏßÉÏĄąÏßÏÂĂżœÚżÎłÌ”Č۞ńŸùŚśłöÁË”śŐûŁșĂżœÚżÎÏßÉό۞ń±ÈÉÏžöÔ”Č۞ńÏ”śa%ŁŹÏßÏŒ۞ń±ÈÉÏžöÔ”Č۞ńÏ”ś![]() a%ŁŹ”œ±ŸÔ”ŚÍłŒÆ·ąÏÖŁŹžĂÏúÊÛÍƶÓÏßÉÏłÉœ»”ĿγÌÊę±ÈÉÏžöÔÂÔöŒÓÁË
a%ŁŹ”œ±ŸÔ”ŚÍłŒÆ·ąÏÖŁŹžĂÏúÊÛÍƶÓÏßÉÏłÉœ»”ĿγÌÊę±ÈÉÏžöÔÂÔöŒÓÁË![]() a%ŁŹÏßÏÂłÉœ»”ĿγÌÊęÉÏÉę”œ1080œÚŁŹŚîÖŐÍƶӔÄÔÂÏúÊÛŚÜ¶îÏßÉϱÈÏßÏÂÉÙÁË54000ÔȘŁŹÇóa”ÄÖ”Łź
a%ŁŹÏßÏÂłÉœ»”ĿγÌÊęÉÏÉę”œ1080œÚŁŹŚîÖŐÍƶӔÄÔÂÏúÊÛŚÜ¶îÏßÉϱÈÏßÏÂÉÙÁË54000ÔȘŁŹÇóa”ÄÖ”Łź
ĄŸŽđ°žĄżŁš1Ł©ĂżœÚżÎ”ÄÏßÉό۞ńÎȘĂżœÚżÎ120ÔȘŁŹÏßÏŒ۞ńÎȘĂżœÚżÎ150ÔȘŁš2Ł©25
ĄŸœâÎöĄż
ąĆžùŸĘÌâÒ⣏ÉèłöÁœžöÎŽÖȘÊ꣏œâ¶țÔȘÒ»ŽÎ·œłÌŚéŒŽżÉÇóœâŁ»ąÆžùŸĘÌâÒ⣏ÁĐłö”ÈÊœŒŽżÉÇóœâ.
Łš1Ł©ÉèžĂ»úččĂżœÚżÎ”ÄÏßÉό۞ńÎȘĂżœÚżÎxÔȘŁŹÏßÏŒ۞ńÎȘĂżœÚżÎyÔȘŁź
ÓÉÌâÒâŁș![]() ŁŹ
ŁŹ
œâ”Ă![]() ŁŹ
ŁŹ
ŽđŁșžĂ»úččĂżœÚżÎ”ÄÏßÉό۞ńÎȘĂżœÚżÎ120ÔȘŁŹÏßÏŒ۞ńÎȘĂżœÚżÎ150ÔȘŁź
Łš2Ł©ÓÉÌâÒâŁș1080ĄÁ150Łš1©![]() a%Ł©©900ĄÁ120Łš1©a%Ł©Łš1+
a%Ł©©900ĄÁ120Łš1©a%Ł©Łš1+![]() a%Ł©=54000ŁŹ
a%Ł©=54000ŁŹ
œâ”Ăa=25Łź
ŽđŁșa”ÄÖ”ÎȘ25Łź



| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹÒŃÖȘ![]() ŁŹ
ŁŹ![]() ÊÇÒ»ŽÎșŻÊę
ÊÇÒ»ŽÎșŻÊę![]() ”ÄÍŒÏóșÍ·Ž±ÈÀęșŻÊę
”ÄÍŒÏóșÍ·Ž±ÈÀęșŻÊę![]() ”ÄÍŒÏó”ÄÁœžöœ»”㣟
”ÄÍŒÏó”ÄÁœžöœ»”㣟
![]() ÇóÖ±Ïß
ÇóÖ±Ïß![]() Óë
Óë![]() Öá”Äœ»”ă
Öá”Äœ»”ă![]() ”ÄŚű±êŒ°
”ÄŚű±êŒ°![]() ”ÄĂæ»ęŁ»
”ÄĂæ»ęŁ»
![]() ÔÚ
ÔÚ![]() ÖáÉÏÊÇ·ńŽæÔÚÒ»”ă
ÖáÉÏÊÇ·ńŽæÔÚÒ»”ă![]() ŁŹÊč”Ă
ŁŹÊč”Ă![]() ”ÄÖ”ŚîŽóŁżÈôŽæÔÚŁŹÖ±œÓĐŽłö”ă
”ÄÖ”ŚîŽóŁżÈôŽæÔÚŁŹÖ±œÓĐŽłö”ă![]() ”ÄŚű±êŁ»ÈôČ»ŽæÔÚŁŹÇë˔ÜÀíÓÉŁ»
”ÄŚű±êŁ»ÈôČ»ŽæÔÚŁŹÇë˔ÜÀíÓÉŁ»
![]() ”±”ă
”±”ă![]() ÔÚË«ÇúÏßÉÏÔ˶ŻÊ±ŁŹŚśÒÔ
ÔÚË«ÇúÏßÉÏÔ˶ŻÊ±ŁŹŚśÒÔ![]() Ąą
Ąą![]() ÎȘÁڱߔÄÆœĐĐËıßĐÎŁŹÇóÆœĐĐËıßĐÎÖÜł€ŚîĐĄÊ±”ă
ÎȘÁڱߔÄÆœĐĐËıßĐÎŁŹÇóÆœĐĐËıßĐÎÖÜł€ŚîĐĄÊ±”ă![]() ”ÄŚű±êŁź
”ÄŚű±êŁź

Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄż¶ÔÓÚÒ»žöčŰÓÚ![]() ”ÄŽúÊęÊœ
”ÄŽúÊęÊœ![]() ,ÈôŽæÔÚÒ»žöÏ”ÊęÎȘŐęÊęčŰÓÚ
,ÈôŽæÔÚÒ»žöÏ”ÊęÎȘŐęÊęčŰÓÚ![]() ”Ä”„ÏîÊœ
”Ä”„ÏîÊœ![]() ,Êč
,Êč![]() ”ÄœáčûÊÇËùÓĐÏ”ÊęŸùÎȘŐûÊę”ÄŐûÊœŁŹÔòłÆ”„ÏîÊœ
”ÄœáčûÊÇËùÓĐÏ”ÊęŸùÎȘŐûÊę”ÄŐûÊœŁŹÔòłÆ”„ÏîÊœ![]() ÎȘŽúÊęÊœ
ÎȘŽúÊęÊœ![]() ”ÄĄ°ŐûÏ””„ÏîÊœĄ± ŁŹÀęÈçŁș
”ÄĄ°ŐûÏ””„ÏîÊœĄ± ŁŹÀęÈçŁș
”±![]() ʱŁŹÓÉÓÚ
ʱŁŹÓÉÓÚ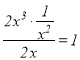 ŁŹčÊ
ŁŹčÊ![]() ÊÇ
ÊÇ![]() ”ÄŐûÏ””„ÏîÊœŁ»
”ÄŐûÏ””„ÏîÊœŁ»
”±![]() ʱŁŹÓÉÓÚ
ʱŁŹÓÉÓÚ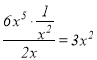 ŁŹčÊ
ŁŹčÊ![]() ÊÇ
ÊÇ![]() ”ÄŐûÏ””„ÏîÊœŁ»
”ÄŐûÏ””„ÏîÊœŁ»
”±![]() ʱŁŹÓÉÓÚ
ʱŁŹÓÉÓÚ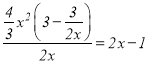 ŁŹčÊ
ŁŹčÊ![]() ÊÇ
ÊÇ![]() ”ÄŐûÏ””„ÏîÊœŁ»
”ÄŐûÏ””„ÏîÊœŁ»
”±![]() ʱŁŹÓÉÓÚ
ʱŁŹÓÉÓÚ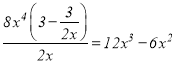 ŁŹčÊ
ŁŹčÊ![]() ÊÇ
ÊÇ![]() ”ÄŐûÏ””„ÏîÊœŁ»
”ÄŐûÏ””„ÏîÊœŁ»
ÏÔÈ»ŁŹ”±ŽúÊęÊœ![]() ŽæÔÚŐûÏ””„ÏîÊœ
ŽæÔÚŐûÏ””„ÏîÊœ![]() ʱŁŹ
ʱŁŹ![]() ÓĐÎȚÊęžöŁŹÏÖ°ŃŽÎÊęŚî”ÍŁŹÏ”ÊęŚîĐĄ”ÄŐûÏ””„ÏîÊœ
ÓĐÎȚÊęžöŁŹÏÖ°ŃŽÎÊęŚî”ÍŁŹÏ”ÊęŚîĐĄ”ÄŐûÏ””„ÏîÊœ![]() ŒÇÎȘ
ŒÇÎȘ![]() ,ÀęÈçŁș
,ÀęÈçŁș![]() .
.
ÔĶÁÒÔÉÏČÄÁÏČąœâŸöÏÂÁĐÎÊÌâŁș
ąĆ.ĆĐ¶ÏŁș”±![]() ʱŁŹ
ʱŁŹ![]()
![]() ”ÄŐûÏ””„ÏîÊœŁšÌÊÇĄ±»òĄ°Č»ÊÇĄ±Ł©Ł»
”ÄŐûÏ””„ÏîÊœŁšÌÊÇĄ±»òĄ°Č»ÊÇĄ±Ł©Ł»
ąÆ.”±![]() ʱŁŹ
ʱŁŹ![]() = ;
= ;
ąÇ.œâ·œłÌŁș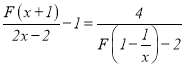 .
.
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
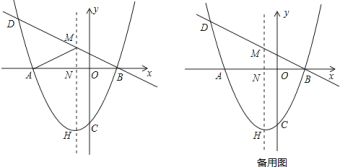
ĄŸÌâÄżĄżÈçÍŒŁŹĆŚÎïÏß![]() œ»
œ»![]() ÖáÓÚ
ÖáÓÚ![]() Ąą
Ąą![]() Áœ”㣏œ»
Áœ”㣏œ»![]() ÖáÓÚ”ă
ÖáÓÚ”ă![]() ŁŹ¶„”ăÎȘ
ŁŹ¶„”ăÎȘ![]() ŁŹÆä¶ÔłÆÖ᜻
ŁŹÆä¶ÔłÆÖ᜻![]() ÖáÓÚ”ă
ÖáÓÚ”ă![]() ŁźÖ±Ïß
ŁźÖ±Ïß![]() Ÿčę
Ÿčę![]() Ąą
Ąą![]() Áœ”㣏œ»ĆŚÎïÏߔĶԳÆÖáÓÚ”ă
Áœ”㣏œ»ĆŚÎïÏߔĶԳÆÖáÓÚ”ă![]() ŁŹÆäÖĐ”ă
ŁŹÆäÖĐ”ă![]() ”ÄșáŚű±êÎȘ
”ÄșáŚű±êÎȘ![]() Łź
Łź
(1)ÇóĆŚÎïÏߔıíŽïÊœŁ»
(2)ÁŹœÓ![]() ŁŹÇó
ŁŹÇó![]() ”ÄÖÜł€Ł»
”ÄÖÜł€Ł»
(3)Èô![]() ÊÇĆŚÎïÏßλÓÚÖ±Ïß
ÊÇĆŚÎïÏßλÓÚÖ±Ïß![]() ”ÄÏ·œÇÒÔÚÆä¶ÔłÆÖáŚóČàÉÏ”ÄÒ»”㣏”±ËıßĐÎ
”ÄÏ·œÇÒÔÚÆä¶ÔłÆÖáŚóČàÉÏ”ÄÒ»”㣏”±ËıßĐÎ![]() ”ÄĂæ»ęŚîŽóʱŁŹÇó”ă
”ÄĂæ»ęŚîŽóʱŁŹÇó”ă![]() ”ÄŚű±êŁź
”ÄŚű±êŁź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹÄł”çĐĆč«ËŸÌáč©ÁË![]() ŁŹ
ŁŹ![]() ÁœÖÖ·œ°ž”ÄÒƶŻÍšŃ¶·ŃÓĂ
ÁœÖÖ·œ°ž”ÄÒƶŻÍšŃ¶·ŃÓĂ![]() ŁšÔȘŁ©ÓëÍš»°Ê±Œä
ŁšÔȘŁ©ÓëÍš»°Ê±Œä![]() Łš·ÖŁ©ÖźŒä”ÄčŰÏ”ŁŹÔòÒÔÏÂË”·šŐęÈ·”ÄÊÇŁš Ł©
Łš·ÖŁ©ÖźŒä”ÄčŰÏ”ŁŹÔòÒÔÏÂË”·šŐęÈ·”ÄÊÇŁš Ł©
ąÙÈôÍš»°Ê±ŒäÉÙÓÚ120·ÖŁŹÔò![]() ·œ°ž±È
·œ°ž±È![]() ·œ°ž±ăÒË
·œ°ž±ăÒË
ąÚÈôÍš»°Ê±ŒäłŹčę200·ÖŁŹÔò![]() ·œ°ž±È
·œ°ž±È![]() ·œ°ž±ăÒË
·œ°ž±ăÒË
ąÛ͚Ѷ·ŃÓĂÎȘ60ÔȘŁŹÔò![]() ·œ°ž±È
·œ°ž±È![]() ·œ°ž”ÄÍš»°Ê±Œä¶à
·œ°ž”ÄÍš»°Ê±Œä¶à
ąÜ”±Íš»°Ê±ŒäÊÇ170·ÖÖÓ/ʱŁŹÁœÖÖ·œ°žÍšŃ¶·ŃÓĂÏà”È
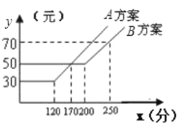
A.1žöB.2žöC.3žöD.4žö
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÌćÓęÆśČÄÊÒÓĐAĄąBÁœÖÖĐÍșĆ”ÄÊ”ĐÄÇòŁŹ1Ö»AĐÍÇòÓë1Ö»BĐÍÇò”ÄÖÊÁżčČ7ǧżËŁŹ3Ö»AĐÍÇòÓë1Ö»BĐÍÇò”ÄÖÊÁżčČ13ǧżËŁź
Łš1Ł©ĂżÖ»AĐÍÇòĄąBĐÍÇò”ÄÖÊÁż·Ö±đÊǶàÉÙǧżËŁż
Łš2Ł©ÏÖÓĐAĐÍÇòĄąBĐÍÇò”ÄÖÊÁżčČ17ǧżËŁŹÔòAĐÍÇòĄąBĐÍÇòžśÓжàÉÙÖ»Łż
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹĆŚÎïÏßy1Łœ(xŁ2)2Ł«mÓëxÖ᜻ÓÚ”ăAșÍBŁŹÓëyÖ᜻ÓÚ”ăCŁŹ”ăDÊÇ”ăCčŰÓÚĆŚÎïÏ߶ԳÆÖá”Ä¶ÔłÆ”ăŁŹÈô”ăA”ÄŚű±êÎȘŁš1ŁŹ0Ł©ŁŹÖ±Ïßy2=kx+bŸčę”ăAŁŹDŁź
Łš1Ł©ÇóĆŚÎïÏß”ÄșŻÊęœâÎöÊœŁ»
Łš2Ł©Çó”ăD”ÄŚű±êșÍÖ±ÏßAD”ÄșŻÊęœâÎöÊœŁ»
Łš3Ł©žùŸĘÍŒÏóÖžłöŁŹ”±xÈĄșÎ֔ʱŁŹy2ŁŸy1Łź

Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÄłĐŁÎȘÁËŽŽœšÊéÏăĐŁÔ°ŁŹÈ„ÄêÓÖčșœűÁËÒ»ĆúÍŒÊ食ŸÁËœâŁŹżÆÆŐÊé”Ä”„ŒÛ±ÈÎÄѧÊé”Ä”„ŒÛ¶à4ÔȘŁŹÓĂ1200ÔȘčșœű”ÄżÆÆŐÊéÓëÓĂ800ÔȘčșœű”ÄÎÄѧÊ鱟ÊęÏà”ÈŁź
Łš1Ł©ÇóÈ„Äêčșœű”ÄÎÄѧÓđșÍżÆÆŐÊé”Ä”„ŒÛžśÊǶàÉÙÔȘŁż
Łš2Ł©ÈôœńÄêÎÄѧÊéșÍżÆÆŐÊé”Ä”„ŒÛșÍÈ„ÄêÏà±È±ŁłÖČ»±äŁŹžĂĐŁŽòËăÓĂ1000ÔȘÔÙčșœűÒ»ĆúÎÄѧÊéșÍżÆÆŐÊ飏ÎÊčșœűÎÄѧÊé55±ŸșóÖÁ¶à»čÄÜčșœű¶àÉÙ±ŸżÆÆŐÊ飿
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹABĄÍBCŁŹDCĄÍBCŁŹEÊÇBCÉÏÒ»”㣏Êč”ĂAEĄÍDEŁ»
Łš1Ł©ÇóÖ€ŁșĄśABEĄŚĄśECDŁ»
Łš2Ł©ÈôAB=4ŁŹAE=BC=5ŁŹÇóCD”Äł€Ł»
Łš3Ł©”±ĄśAEDĄŚĄśECDʱŁŹÇëĐŽłöÏ߶ÎADĄąABĄąCDÖźŒäÊęÁżčŰÏ”ŁŹČąË”ĂśÀíÓÉŁź

Č鿎Žđ°žșÍœâÎö>>
čúŒÊѧУÓĆŃĄ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com