
【题目】如图,抛物线y1=(x-2)2+m与x轴交于点A和B,与y轴交于点C,点D是点C关于抛物线对称轴的对称点,若点A的坐标为(1,0),直线y2=kx+b经过点A,D.
(1)求抛物线的函数解析式;
(2)求点D的坐标和直线AD的函数解析式;
(3)根据图象指出,当x取何值时,y2>y1.

【答案】(1)y1=(x﹣2)2﹣1;(2)y=x﹣1;(3)当1<x<4时.
【解析】
(1)把点A的坐标代入抛物线解析式可求出m的值,进而可得到抛物线的解析式;(2)首先由抛物线的解析式可求出点C的坐标,再根据函数图象的对称性即可求出点D的坐标;由于点A的坐标已知,进而可求出直线AD的解析式;(3)结合两个函数图象可知当直线在抛物线上方时可得到y2>y1的解集.
解:
(1)∵点A(1,0)在抛物线上,
∴(1﹣2)2+m=0,
∴m=﹣1,
∴y1=(x﹣2)2﹣1;
(2)抛物线y1=(x﹣2)2﹣1的对称轴为x=2,与y的交点C的坐标为(0,3),
∵点D是点C关于对称轴x=2的对称点,
∴点D的坐标为(4,3),
直线AD经过点点A,D,
∴![]() ,
,
解得k=1,b=﹣1,
∴y=x﹣1;
(3)当1<x<4时,y2>y1.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=40°,则∠CDE的度数为( )
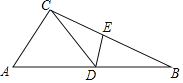
A.50°B.40°C.60°D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,且经
,且经![]() 、
、![]() 两点.
两点.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 在抛物线的对称轴
在抛物线的对称轴![]() 上,是否存在点
上,是否存在点![]() ,使它到点
,使它到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小,如果存在求出点
的距离之和最小,如果存在求出点![]() 的坐标,如果不存在请说明理由.
的坐标,如果不存在请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“互联网+”时代的到来,传统的教学模式也在悄然发生着改变.某出国培训机构紧跟潮流,对培训课程采取了线上线下同步销售的策路,为了让客户更理性的选择,该机构推出了甲、乙两个课程体验包:甲课程体验包价值660元含3节线上课程和2节线下课;乙课程体验包价值990元含2节线上课程和5节线下课程.
(1)分别求出该机构每节课的线上价格和线下价格;
(2)该机构其中一个销售团队上个月的销售业绩为:线上课程成交900节,线下课成交1000节.为回馈客户,本月该机构针对线上、线下每节课程的价格均作出了调整:每节课线上价格比上个月的价格下调a%,线下价格比上个月的价格下调![]() a%,到本月底统计发现,该销售团队线上成交的课程数比上个月增加了
a%,到本月底统计发现,该销售团队线上成交的课程数比上个月增加了![]() a%,线下成交的课程数上升到1080节,最终团队的月销售总额线上比线下少了54000元,求a的值.
a%,线下成交的课程数上升到1080节,最终团队的月销售总额线上比线下少了54000元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组在探索“各内角都相等的圆内接多边形是否为正多边形”时,进行如下讨论:
甲同学:这种多边形不一定是正多边形,如圆内接矩形.
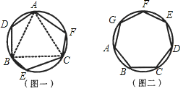
乙同学:我发现边数是![]() 时,它也不一定是正多边形,如图
时,它也不一定是正多边形,如图![]() ,
,![]() 是正三角形,
是正三角形,![]() ,证明六边形
,证明六边形![]() 的各内角相等,但它未必是正六边形.
的各内角相等,但它未必是正六边形.
丙同学:我能证明,边数是![]() 时,它是正多边形,我想…,边数是
时,它是正多边形,我想…,边数是![]() 时,它可能也是正多边形.
时,它可能也是正多边形.
![]() 请你说明乙同学构造的六边形各内角相等;
请你说明乙同学构造的六边形各内角相等;
![]() 请你证明,各内角都相等的圆内接七边形
请你证明,各内角都相等的圆内接七边形![]() (如图
(如图![]() )是正七边形;(不必写已知,求证)
)是正七边形;(不必写已知,求证)
![]() 根据以上探索过程,提出你的猜想.(不必证明)
根据以上探索过程,提出你的猜想.(不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小泽和小帅两同学分别从甲地出发,骑自行车沿同一条路到乙地参加社会实践活动.如图折线OAB和线段CD分别表示小泽和小帅离甲地的距离y(单位:千米)与时间x(单位:小时)之间函数关系的图象.根据图中提供的信息,解答下列问题:
(1)小帅的骑车速度为 千米/小时;点C的坐标为 ;
(2)求线段AB对应的函数表达式;
(3)当小帅到达乙地时,小泽距乙地还有多远?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点为对称中心,把点A(3,4)逆时针旋转90°,得到点B,则点B的坐标为()
A. (4,-3) B. (-4,3) C. (-3,4) D. (-3,-4)
查看答案和解析>>
科目:初中数学 来源: 题型:
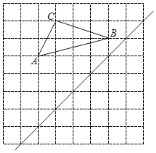
【题目】如图,在8×8的正方形网格中,每个小正方形的边长都是1,已知△ABC的三个顶点在格点上.
(1)画出△ABC关于直线l对称的△A1B1C1;
(2)在直线l上找一点P,使PA+PB的长最短;(不写作法,保留作图痕迹)
(3)△ABC 直角三角形(填“是”或“不是”),并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC中,AB=AC,∠BAC=120,
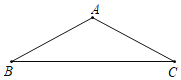
(1)利用直尺、圆规,求作AB的垂直平分线DE,交BC于点D、交AB于点E:(不要求写出作法,但要求保留作图痕迹)
(2)若BD=3,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com