
【题目】如图,已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,且经
,且经![]() 、
、![]() 两点.
两点.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 在抛物线的对称轴
在抛物线的对称轴![]() 上,是否存在点
上,是否存在点![]() ,使它到点
,使它到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小,如果存在求出点
的距离之和最小,如果存在求出点![]() 的坐标,如果不存在请说明理由.
的坐标,如果不存在请说明理由.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果以13元/千克的价格销售,那么每天可售出240千克.
小红:通过调查验证,我发现每天的销售量y(千克)与销售单价x(元)之间存在一次函数关系,每天销售200千克以上.
(1)求每天的销售量y(千克)与销售单价x(元)之间的函数关系式;
(2)该超市销售这种水果每天获取的利润达到1040元,那么销售单价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一期间,小明一家一起去旅游,如图是小明设计的某旅游景点的图纸(网格是由相同的小正方形组成的,且小正方形的边长代表实际长度100m),在该图纸上可看到两个标志性景点A,B.若建立适当的平面直角坐标系,则点A(-3,1),B(-3,-3),第三个景点C(3,2)的位置已破损.
(1)请在图中标出景点C的位置;
(2)小明想从景点B开始游玩,途经景点A,最后到达景点C,求小明一家最短的行走路程(参考数据:![]() ≈6,结果保留整数).
≈6,结果保留整数).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个关于![]() 的代数式
的代数式![]() ,若存在一个系数为正数关于
,若存在一个系数为正数关于![]() 的单项式
的单项式![]() ,使
,使![]() 的结果是所有系数均为整数的整式,则称单项式
的结果是所有系数均为整数的整式,则称单项式![]() 为代数式
为代数式![]() 的“整系单项式” ,例如:
的“整系单项式” ,例如:
当![]() 时,由于
时,由于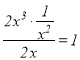 ,故
,故![]() 是
是![]() 的整系单项式;
的整系单项式;
当![]() 时,由于
时,由于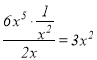 ,故
,故![]() 是
是![]() 的整系单项式;
的整系单项式;
当![]() 时,由于
时,由于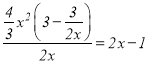 ,故
,故![]() 是
是![]() 的整系单项式;
的整系单项式;
当![]() 时,由于
时,由于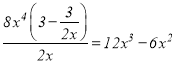 ,故
,故![]() 是
是![]() 的整系单项式;
的整系单项式;
显然,当代数式![]() 存在整系单项式
存在整系单项式![]() 时,
时,![]() 有无数个,现把次数最低,系数最小的整系单项式
有无数个,现把次数最低,系数最小的整系单项式![]() 记为
记为![]() ,例如:
,例如:![]() .
.
阅读以上材料并解决下列问题:
⑴.判断:当![]() 时,
时,![]()
![]() 的整系单项式(填“是”或“不是”);
的整系单项式(填“是”或“不是”);
⑵.当![]() 时,
时,![]() = ;
= ;
⑶.解方程: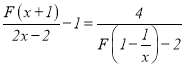 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要建一个如图所示的面积为300![]() 的长方形围栏,围栏总长50m,一边靠墙(墙长25m),
的长方形围栏,围栏总长50m,一边靠墙(墙长25m),

(1)求围栏的长和宽;
(2)能否围成面积为400 ![]() 的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由。
的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
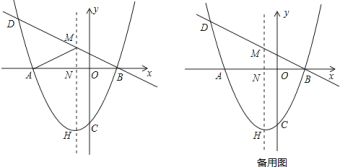
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,顶点为
,顶点为![]() ,其对称轴交
,其对称轴交![]() 轴于点
轴于点![]() .直线
.直线![]() 经过
经过![]() 、
、![]() 两点,交抛物线的对称轴于点
两点,交抛物线的对称轴于点![]() ,其中点
,其中点![]() 的横坐标为
的横坐标为![]() .
.
(1)求抛物线的表达式;
(2)连接![]() ,求
,求![]() 的周长;
的周长;
(3)若![]() 是抛物线位于直线
是抛物线位于直线![]() 的下方且在其对称轴左侧上的一点,当四边形
的下方且在其对称轴左侧上的一点,当四边形![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
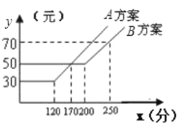
【题目】如图,某电信公司提供了![]() ,
,![]() 两种方案的移动通讯费用
两种方案的移动通讯费用![]() (元)与通话时间
(元)与通话时间![]() (分)之间的关系,则以下说法正确的是( )
(分)之间的关系,则以下说法正确的是( )
①若通话时间少于120分,则![]() 方案比
方案比![]() 方案便宜
方案便宜
②若通话时间超过200分,则![]() 方案比
方案比![]() 方案便宜
方案便宜
③通讯费用为60元,则![]() 方案比
方案比![]() 方案的通话时间多
方案的通话时间多
④当通话时间是170分钟/时,两种方案通讯费用相等
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=(x-2)2+m与x轴交于点A和B,与y轴交于点C,点D是点C关于抛物线对称轴的对称点,若点A的坐标为(1,0),直线y2=kx+b经过点A,D.
(1)求抛物线的函数解析式;
(2)求点D的坐标和直线AD的函数解析式;
(3)根据图象指出,当x取何值时,y2>y1.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成,需支付运费4800元.已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少200元.
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟?
(2)若单独租用一台车,租用哪台车合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com